Bonjour, je sèche complètement, j'aurais besoin de votre aide pour cette exo.
Soit f la fonction définie sur IR par f(x)= e^x-x-1
a) Établir le tableau de variation de la fonction f.
j'ai trouver que la fonction etais strictement positive et tandais donc vers plus infini
b) Dans un repère, construire la courbe représentative de la fonction et de la droite d'équations y=-x-1
je l'es faite grace a la calculatrice
c) Soit à un réel. Écrire en fonction de a, une équation de la tangente T à la courbe C au point M d'abscisse a.
sachant que T=f'(a)(x-a)+f(a)
alors f'(x)=e^x-x et f(x)=e^x-x-1 donc T=f'(x)(x-x)+f(x)=e^x-x(x-x)+(e^x-x-1)=e^x-x+e^x-x-1=e^x+e^x-1=2e^x-1
d) T coupe D au point N d'anbscisse b. Établir que b-a=-1
e) En déduire une construction, à effectuer dans le même repére, de la tangente T à C au point M d'abscisse 1,5. On fera apparaître le point N correspondant.
DM propriété d'une tangente
9 messages
- Page 1 sur 1
Happytime a écrit:D'accord tant pis ======> NON ! ! ! pas tant pis ! ! !
Bjr, je te sent perdu....
as-tu trouvé ça, déjà ?....http://www.cjoint.com/c/ELvnjUhtvMf et http://www.cjoint.com/c/ELvnioHeaHf
c) Soit à un réel. Écrire en fonction de a, une équation de la tangente T à la courbe C au point M d'abscisse a.
sachant que T=f'(a)(x-a)+f(a)
alors f'(x)=e^x-x et f(x)=e^x-x-1 donc T=f'(x)(x-x)+f(x)=e^x-x(x-x)+(e^x-x-1)=e^x-x+e^x-x-1=e^x+e^x-1=2e^x-1
d) T coupe D au point N d'anbscisse b. Établir que b-a=-1
pour trouver la fameuse tangente :
y = f ' (a) (x-a) + f(a)
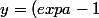(x-a) + exp{a} - a - 1)
on développe...
=====>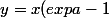 - 1 + exp{a}(1 - a))
et si on cherche l'intersection (" = ") entre cette tangente et D d'équation y = - x - 1 :
on fait :
 - 1 + exp{a}(1 - a) = - x - 1)
avec une intersection en N d'abscisse b :

====>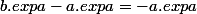
 = - exp{a})
on multiplie de chaque côté de l'égalité par :
:
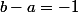 , cqfd.
, cqfd.
sachant que T=f'(a)(x-a)+f(a)
alors f'(x)=e^x-x et f(x)=e^x-x-1 donc T=f'(x)(x-x)+f(x)=e^x-x(x-x)+(e^x-x-1)=e^x-x+e^x-x-1=e^x+e^x-1=2e^x-1
d) T coupe D au point N d'anbscisse b. Établir que b-a=-1
pour trouver la fameuse tangente :
y = f ' (a) (x-a) + f(a)
on développe...
=====>
et si on cherche l'intersection (" = ") entre cette tangente et D d'équation y = - x - 1 :
on fait :
avec une intersection en N d'abscisse b :
====>
on multiplie de chaque côté de l'égalité par
laetidom a écrit:c) Soit à un réel. Écrire en fonction de a, une équation de la tangente T à la courbe C au point M d'abscisse a.
sachant que T=f'(a)(x-a)+f(a)
alors f'(x)=e^x-x et f(x)=e^x-x-1 donc T=f'(x)(x-x)+f(x)=e^x-x(x-x)+(e^x-x-1)=e^x-x+e^x-x-1=e^x+e^x-1=2e^x-1
d) T coupe D au point N d'anbscisse b. Établir que b-a=-1
pour trouver la fameuse tangente :
y = f ' (a) (x-a) + f(a)
on développe...
=====>
et si on cherche l'intersection (" = ") entre cette tangente et D d'équation y = - x - 1 :
on fait :
avec une intersection en N d'abscisse b :
====>
on multiplie de chaque côté de l'égalité par:
, cqfd.
Merci beaucoup pour ton aide
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
