Projection sur un plan

[posso49]

Bonjour, je cherche le lieu des droites issues d'un point fixe O sur lesquelles deux segments donnés AB et CD ont des projections orthogonales égales.
J'ai bien trouvé par géospace qu'il s'agit d'un plan passant par O, mais je ne vois pas comment le déterminer.
Merci pour votre aide.

[Ben314]

Salut,

Bonjour, je cherche le lieu des droites issues d'un point fixe O sur lesquelles deux segments donnés AB et CD ont des projections orthogonales égales.
J'ai bien trouvé par géospace qu'il s'agit d'un plan passant par O, mais je ne vois pas comment le déterminer.
Merci pour votre aide.

Je comprend rien à ta prose.
Déjà, si tu cherche "les droite passant par O telles que", je vois pas comment tu pourrait avoir des segments donnés sur ces droites (inconnues).
Ensuite, "des projection orthogonales égales", je vois pas non plus ce que ça signifie : tu projette sur quoi ? c'est quoi qui doit être égal ? (les segments images de ceux de départ par la projection ?)

Bref, est-ce que tu peut faire un truc compréhensible du style :
- Au début on a ça ça ça et ça de fixés (= connus)
- Partant de ça et ça variable, on construit tel truc puis tel autre, etc..
- Et on veut qu'au final on ait telle propriété qui soit vérifiée.

[posso49]

Ce n'est pas ma prose, c'est le texte exact du problème. Pour moi il me parait clair.
Au départ, on a un point O et deux segments AB et CD.
On cherche les droites qui passent par O sur lesquelles les projections orthogonales de AB et CD forment deux segments égaux.
J'ai trouvé que l'ensemble de ces droites forment un plan passant par O.
Je voudrais savoir comment se situe ce plan par rapport à AB et CD et comment construire ces droites manuellement.

[posso49]

jj.jpg

[Ben314]

J'ai toujours l'impression de pas bien comprendre grand chose...
Comme l'image d'un segment [AB] par la projection orthogonale sur une droite (d), c'est le segment [A',B'] où A' et B' sont les projetés de A et B, pour que [AB] et [CD] aient la même projection, il faut (et il suffit) que A'=C' et B'=D' ou bien que A'=D' et B'=D'.
Si on regarde le 1er cas avec A'=C' et B'=D', ça signifie que A et C ont été projeté suivant la droite (AC) dont que la droite (d) sur laquelle on projette est perpendiculaire et concourante à (AC) et, pour la même raison, (d) doit aussi être perpendiculaire et concourante à (BD). Sauf que des droite perpendiculaire et concourante à deux droites données, il n'y en a qu'une seule et qu'il est plus que probable que cette dernière ne passe pas par O.
Donc en général, il n'y a aucune solution au problème.

[posso49]

Bonjour Ben.
Je suis très étonné que tu ne comprennes pas le problème. L'énoncé me parait pourtant très clair ainsi que l'exemple fourni et réalisé sur geospace.
D'abord, il n'est pas demandé que [AB] et [CD] aient la même projection, mais des projections égales.
Et comme tu peux le voir sur le schéma, [AB] et [CD] se projettent sur une droite en [A1B1] et [C1D1] et
[A1B1] = [C1D1] et sur une autre droite en [A2B2] et [C2D2] avec [A2B2] = [C2D2]. Ces deux droites passent par O. Elles forment un plan et sur toutes les droites de ce plan passant par O, les projections de [AB] et [CD] sont égales. J'ai vérifié avec la droite variable (OX) sur laquelle je n'ai pas fait apparaitre les projections pour ne pas surcharger.
Je cherche à définir la position de ce plan par rapport aux segments [AB] et [CD], mais peut être que la seule réponse est que le lieu de ces droites est un plan.

[Tiruxa47]

Bonjour,
Juste une réflexion, dans le cas où les vecteurs AB et CD ne sont pas colinéaires ils forment une base d'un plan, il existe donc un vecteur n orthogonal aux vecteurs AB et CD.
Sur la droite (D) passant par O et de vecteur directeur n les projections des deux segments en question sont de longueur nulle. Donc la droite (D) fait partie du lieu.

[chan79]

salut
Un cas particulier:
On place un repère orthonormé (O,I,J,K)
A(1,0,0)
B(2,0,0)
C(0,1,0)
D(0,2,0)
[AB] et [CD] ont les mêmes projetés sur la droite
[AB] et [CD] ont les mêmes projetés sur la droite
[AB] et [CD] ont les mêmes projetés sur la droite

[Ben314]

D'abord, il n'est pas demandé que [AB] et [CD] aient la même projection, mais des projections égales.

??????????
Tu pourrait un peu préciser ce que tu entend par "égal" vu que ta prose semble sous entendre que, selon toi, que deux choses peuvent être "égales" sans être "les mêmes" ?

[Ben314]

Ah, en lisant l'exemple de Chan, je comprend le problème : visiblement, tu confond la notion de segment et celle de vecteurs : ce que tu veut, c'est que les segments en question soient de même sens et de même longueur ce qui est évidement bien différent de "être égal".
Rappelons (au cas où...) qu'un segment, c'est un ensemble de points et que deux ensemble sont "égaux" lorsqu'ils ont exactement les mêmes éléments donc il n'y a pas la moindre ambiguïté concernant le sens à donner à "deux segments égaux". Et si on veut dire qu'ils sont de même sens et de même longueur, ben soit on écrit "de même sens et de même longueur", soit si on connait la notion, ben on écrit que les vecteurs doivent être égaux.

Et pour revenir au problème, étant donné deux vecteurs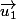 et 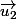d'un e.v. euclidien de dim quelconque, si tu cherche les vecteurs tels que les projetés orthogonaux de 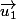et 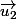sur la droite vectorielle engendré par soient les même, c'est précisément ceux qui sont orthogonaux à .
Donc le plan affine que tu cherche, c'est celui passant par O et de vecteur normal (ou celui dirigé par si tu accepte que les projetés des vecteurs soient l'opposé l'un de l'autre, c'est à dire que les segments aient même longueur, mais pas le même sens).