LaylaManga a écrit:Je viens de faire un truc mais je ne sais pas si c'est ça.. En fit, j'ai tout laisser jusqu'au whileend (en enlevant le U) et au lieu de mettre quelque chose pour le disp j'ai juste laisser A/N entrée et stop et quand je fais pour l'exercice , quand je tappe 500 je trouve 169/500 et pour 1000 je trouve 327/1000 mais après je suppose que c'est aléatoire.. Est-ce que se serait ça?? Mais alors comment je répond a mon problème de l'exercice , quand il faut déduire l'aire sous la parabole???
Il s'agit de la méthode de Monte-Carlo inventée par Von Neumann
que je te détaille vite fait:
on dispose d'un carré unité que l'on bombarde
avec des points aléatoires M(ran#,ran#)
l'aire

du domaine sous la courbe est approchée par le quotient A/N,
l'aire du domaine
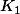
au dessus de la parabole est approchée par K/N
K/N+A/N=1,
la limite du quotient A/N , quand N tend vers

est l'aire

le souci, cest que la suite A_N=A/N converge très lentement.
Peut être dois tu renseigner N=10 000 et faire tourner la calculatrice longtemps,
pour obtenir les trois premières décimales de la limite.
à toi de deviner de quel nombre il s'agit, quand N devient grand et que l'on passe à la limite.
ps1: pour les connaisseurs, je comprends pas très bien comment
la méthode de Monte-Carlo est compatible avec le théorème de Pick... ??
ps2: du coup, le display du quotient A/N devrait se faire dans la boucle
