Programme de Seconde ?
Titux a écrit:Ok Lostounet !
Soit n (appartenant à N) le nombre darticles vendus pour un prix p. Pose
Par hypothèseest fonction linéaire de
Essaie d'exprimer delta N en fonction de delta p et d'exprimer n en fonction de p ensuite.
Je t'aide ensuite !
Désolé, mais je ne comprends pas vraiment la méthode que tu as proposée, c'est pour cela que je pose cette question.
Et je ne vois justement pas comment exprimer p - 75 en fonction de n - 100, qui sont deux choses différentes, si c'est ce qui est demandé.
Merci de m'aider!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Tu as bien compris que l'on va ici déterminer le nombre d'articles vendus n en fonction du prix p ?
Dans l'énoncé, on te parle de différences. Tu utilises donc les deltas.
Pourquoi à ton avis peut on écrire que delta n = -4 delta p ?
Ou sinon expose moi ta méthode, elle est peut être très bien aussi.
Dans l'énoncé, on te parle de différences. Tu utilises donc les deltas.
Pourquoi à ton avis peut on écrire que delta n = -4 delta p ?
Ou sinon expose moi ta méthode, elle est peut être très bien aussi.
Titux a écrit:Tu as bien compris que l'on va ici déterminer le nombre d'articles vendus n en fonction du prix p ?
Dans l'énoncé, on te parle de différences. Tu utilises donc les deltas.
Pourquoi à ton avis peut on écrire que delta n = -4 delta p ?
Ou sinon expose moi ta méthode, elle est peut être très bien aussi.
Ma méthode est très incomplète et n'aboutit pas, donc je ne l'appellerais pas une méthode:
J'ai supposé qu'il y a 3 "tarifs".
Les fonctions modélisent le prix d'un article -> profit total.
f(75) = 75 * 100 - 100 * 30
= 4500
f (75 + n) = (100 - y) (-25 + 2n)
f (75 - n) = (100 + y) (45 - n)
n = 5; 10; 15.. (multiples de 5)
y = 20; 40.. (multiples de 20)
Mais après, ça ne va pas bien loin.. :ptdr:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Salut !
Vu que tu as vu les domaines de définition, considérons le système :

Il est vrai que si l'on ne demande pas d'expliciter le domaine, on se contentera de et
et 
Par contre si on demande de l'expliciter, comment faire ?
Tout d'abord, on remarque le système est défini si et seulement si et
et  . Or ce système se résous dans
. Or ce système se résous dans  et donc on cherche des couples par conséquent :
et donc on cherche des couples par conséquent :
,(x;-2)\}) .Ensuite pour résoudre ce système, tu effectue ce que l'on appelle un changement de variable :
.Ensuite pour résoudre ce système, tu effectue ce que l'on appelle un changement de variable :
Tu pose et
et  et tu résous le système
et tu résous le système  puis lorsque tu as trouvé X et Y tu remplaces ces valeurs par les expressions définie au départ.
puis lorsque tu as trouvé X et Y tu remplaces ces valeurs par les expressions définie au départ.
Voilà, c'était une petite parenthèse ^^.
Vu que tu as vu les domaines de définition, considérons le système :
Il est vrai que si l'on ne demande pas d'expliciter le domaine, on se contentera de
Par contre si on demande de l'expliciter, comment faire ?
Tout d'abord, on remarque le système est défini si et seulement si
Tu pose
Voilà, c'était une petite parenthèse ^^.
Voilà, enfin terminé mon examen régional, LIBERTÉ §§§ :we: ( foiré l'histoire/géo aussi mais bon )
Donc je continue mon mini-cours :
Équivalences :
Une équivalence ( ) est définie par :
) est définie par :  \Leftrightarrow \left( \left( P \Rightarrow Q \right) \wedge \left( Q \Rightarrow P \right) \right) \Leftrightarrow \left( \left( P \wedge Q \right) \vee \left( \neg P \wedge \neg Q \right) \right)) .
.
D'après la définition, une équivalence est vraie si et seulement si ( le jeu de mots : "si et seulement si" = "équivalence" ^^ ) P et Q sont toutes les deux vraies, ou P et Q toutes les deux fausses . En gros, une équivalence est vraie lorsque P et Q ont la même valeur de vérité . Vulgairement, c'est comme le symbole "=" mais pour les valeurs de vérité des propositions ( P Q veut dire que P est équivalent à Q, mais aussi que la valeur de vérité de P est égale à la valeur de vérité de Q ) .
Ou alors, on peut aussi dire qu'elle n'est vraie que s'il y a double implication ( que si P implique Q, et Q implique P ) .
Équivalences successives :
T'as toujours l'implication suivante :
 \Rightarrow \left( P_1 \Leftrightarrow P_n \right)) .
.
Montrer une équivalence :
Donc pour montrer qu'une équivalence est vraie, soit tu montres qu'il y a double implication, soit tu procédes par équivalences successives, soit tu montres que "P et Q" ou "NON P et NON Q" est vraie .
Donc je continue mon mini-cours :
Équivalences :
Une équivalence (
D'après la définition, une équivalence est vraie si et seulement si ( le jeu de mots : "si et seulement si" = "équivalence" ^^ ) P et Q sont toutes les deux vraies, ou P et Q toutes les deux fausses . En gros, une équivalence est vraie lorsque P et Q ont la même valeur de vérité . Vulgairement, c'est comme le symbole "=" mais pour les valeurs de vérité des propositions ( P Q veut dire que P est équivalent à Q, mais aussi que la valeur de vérité de P est égale à la valeur de vérité de Q ) .
Ou alors, on peut aussi dire qu'elle n'est vraie que s'il y a double implication ( que si P implique Q, et Q implique P ) .
Équivalences successives :
T'as toujours l'implication suivante :
Montrer une équivalence :
Donc pour montrer qu'une équivalence est vraie, soit tu montres qu'il y a double implication, soit tu procédes par équivalences successives, soit tu montres que "P et Q" ou "NON P et NON Q" est vraie .
Ah oui, petite parenthèse encore.
Je t'ai parlé de système de trois équations à trois inconnues :
C'est le même principe qu'avec les système de deux équations à deux inconnues mais à une différence près que les déterminant contiennent trois nombre sur trois lignes :
Considérons :
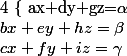
Le déterminant D du système sera :
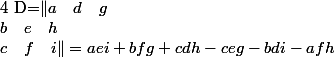
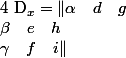
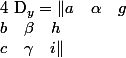
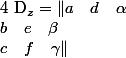
Si tu remarque bien, dans le calcul des détermiant,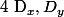 et
et 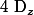 la colonne
la colonne 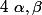 et
et 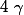 remplace toujours la colonne des coefficient correspondant à l'indice du déterminant.
remplace toujours la colonne des coefficient correspondant à l'indice du déterminant.
Ensuite même démarche sauf que si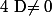 alors :
alors :
=\(\frac{D_x}{D},\frac{D_y}{D},\frac{D_z}{D}\))
et si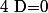 alors il existe deux réels réel
alors il existe deux réels réel 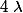 et
et 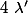 tel que :
tel que :
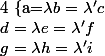 .
.
Il faut donc regarder si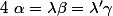 .
.
Si c'est le cas alors il y a une infinité de solutions sinon aucune.
Je t'ai parlé de système de trois équations à trois inconnues :
C'est le même principe qu'avec les système de deux équations à deux inconnues mais à une différence près que les déterminant contiennent trois nombre sur trois lignes :
Considérons :
Le déterminant D du système sera :
Si tu remarque bien, dans le calcul des détermiant,
Ensuite même démarche sauf que si
et si
Il faut donc regarder si
Si c'est le cas alors il y a une infinité de solutions sinon aucune.
@benekire2 : je l'ai fait souvent jusqu'à ce que mon prof m'a dit d'éviter car les élèves ne comprenaient rien ^^ Sinon, bah c'est pas hyper dur ( enfin, ça dépend de l'énoncé ), faut juste être un peu plus rigoureux, savoir manier les lois de distributivité/associativité, ainsi que la loi de Morgan, et aussi connaître le principe du tiers exclu . En gros, le travail consiste à trouver que ( (P et Q) ou (non P et nonQ) ) <=> ( A ou nonA ou ( d'autres truc dont on s'en fou ) ), et on conclut avec le principe du tiers exclu .
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
