Produit scalaire
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
maths675452
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Déc 2013, 19:44
-
 par maths675452 » 30 Mar 2014, 12:46
par maths675452 » 30 Mar 2014, 12:46
ABCD est un rectangle directeur tel que AB= 3 et AD=4. E est le milieu de [BC]
CBF est un triangle direct rectangle et isocèle en F
1.
A. Faire une figure puis calculer la longueur BF
B. Calculer les produits scalaires suivants : BC.BF , BC.AB , AB.BF (vecteurs)
C. En écrivant AC et AF (vecteurs) comme somme de vecteurs bien choisis et en utilisant la question précédente , calculer la valeur exacte de AC.AF (c'est là où je bloque...)
2. En utilisant un repère orthonormé soigneusement choisi (que vous ferez apparaître sur le dessin) retrouver la valeur de AC.AF(vecteurs) > j'ai trouvé -2 et je ne sais pas du coup si c'est le bon résultat
Pouvez vous m'aider..?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Mar 2014, 13:07
par chan79 » 30 Mar 2014, 13:07
Salut
Montre la figure que tu as dessinée. Pour BF, il faut penser à un théorème assez connu ... :zen:
-
maths675452
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Déc 2013, 19:44
-
 par maths675452 » 30 Mar 2014, 13:14
par maths675452 » 30 Mar 2014, 13:14
j'ai fait un rectangle ABCD de longueur 4 et de largeur 3
De ce type :
A B
D C
et j'ai mis F à droite de sorte que BCF soit rectangle isocèle en F (pas la possibilité de faire de photo rapide..)
pour BF j'ai déjà fait Pythagore mais c'est à partir de la question c/ que je bloque..

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Mar 2014, 13:38
par chan79 » 30 Mar 2014, 13:38
maths675452 a écrit:j'ai fait un rectangle ABCD de longueur 4 et de largeur 3
De ce type :
A B
D C
et j'ai mis F à droite de sorte que BCF soit rectangle isocèle en F (pas la possibilité de faire de photo rapide..)
pour BF j'ai déjà fait Pythagore mais c'est à partir de la question c/ que je bloque..
ABCD doit être direct (sens contraire des aiguilles d'une montre)
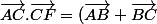.( \vec{CB}.\vec{BF}))
-
maths675452
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Déc 2013, 19:44
-
 par maths675452 » 30 Mar 2014, 13:46
par maths675452 » 30 Mar 2014, 13:46
ahoui.. les résultats que j'ai obtenus restent inchangés?
Pour la c/ c'est le produit scalaire : AC.AF

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Mar 2014, 13:50
par chan79 » 30 Mar 2014, 13:50
maths675452 a écrit:ahoui.. les résultats que j'ai obtenus restent inchangés?
Pour la c/ c'est le produit scalaire : AC.AF
alors comme ça:
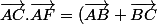.( \vec{AB}+\vec{BF}))
-
maths675452
- Membre Naturel
- Messages: 29
- Enregistré le: 29 Déc 2013, 19:44
-
 par maths675452 » 30 Mar 2014, 13:59
par maths675452 » 30 Mar 2014, 13:59
je trouve un truc incohérent.. :
(AB,BC).(AB,BF) = AB.AB + AB.BF + BC.AB + BC.BF
= AB² + ABxBF x cos ABF + 0 + BCx BF x cos CBF
= 9 + 3 x 2 x cos (90+45 = 135 : impossible à faire) + 4 x 2 x cos 45

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Mar 2014, 18:13
par chan79 » 30 Mar 2014, 18:13
maths675452 a écrit:je trouve un truc incohérent.. :
(AB,BC).(AB,BF) = AB.AB + AB.BF + BC.AB + BC.BF
= AB² + ABxBF x cos ABF + 0 + BCx BF x cos CBF
= 9 + 3 x 2 x cos (90+45 = 135 : impossible à faire) + 4 x 2 x cos 45
Mets tes résultats de la question b.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
