Produit scalaire.
26 messages
- Page 1 sur 2 - 1, 2
Produit scalaire.
Bonjour tout le monde,
J'ai du mal à saisir ce qu'il faut faire dans cet exercice, donc si quelqu'un pourrait m'éclaircir merci d'avance
ABCD est un carré avec AB=2, déterminez les ensembles suivants:
(C1)= {M;) P/ AM.AB= 2} (tout en vecteur)
(C2)= {M ;)P/ BM.CD= -4} (vecteurs)
(C3)= {M;)P / MA²-MB²= 12 }
(C4)= {M;)P / MA²-MC²= -8 }
J'ai du mal à saisir ce qu'il faut faire dans cet exercice, donc si quelqu'un pourrait m'éclaircir merci d'avance
ABCD est un carré avec AB=2, déterminez les ensembles suivants:
(C1)= {M;) P/ AM.AB= 2} (tout en vecteur)
(C2)= {M ;)P/ BM.CD= -4} (vecteurs)
(C3)= {M;)P / MA²-MB²= 12 }
(C4)= {M;)P / MA²-MC²= -8 }
Salut !
Il faut déterminer la nature des ensembles suivant et pourquoi pas, les représenter :++:
Par exemple, est une droite (encore faut-il le prouver) :we:
est une droite (encore faut-il le prouver) :we:
Dans ton dernier ensemble, on n'a pas le membre de droite...
Rimchi a écrit:Bonjour tout le monde,
J'ai du mal à saisir ce qu'il faut faire dans cet exercice, donc si quelqu'un pourrait m'éclaircir merci d'avance
ABCD est un carré avec AB=2, déterminez les ensembles suivants:
(C1)= {M;) P/ AM.AB= 2} (tout en vecteur)
(C2)= {MP/ BM.CD= -4} (vecteurs)
(C3)= {M;)P / MA²-MB²= 12 }
(C4)= {M;)P / MA²-MC²= - }
Il faut déterminer la nature des ensembles suivant et pourquoi pas, les représenter :++:
Par exemple,
Dans ton dernier ensemble, on n'a pas le membre de droite...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
Il faut déterminer la nature des ensembles suivant et pourquoi pas, les représenter :++:
Par exemple,est une droite (encore faut-il le prouver) :we:
Dans ton dernier ensemble, on n'a pas le membre de droite...
Oui mais je ne sais pas comment m'y prendre, ne faut-il pas que je trouve d'abbord les coordonées du vecteur AB puis AM pour compter leur produit? ..
Ah oups merci j'ai modifié
Rimchi a écrit:Oui mais je ne sais pas comment m'y prendre, ne faut-il pas que je trouve d'abbord les coordonées du vecteur AB puis AM pour compter leur produit? ..
Ah oups merci j'ai modifié
Attention !
Le produit scalaire n'est pas, comme on pourrait le penser, un produit de vecteur.
On a
Pour trouver cette ensemble, on va faire intervenir le point
Tu peux maintenant faire quelque chose :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
@Rimchi
Une des méthodes est de se placer dans un repère orthonormé de (plan euclidien)
(plan euclidien)
et de travailler avec les coordonnées des points et les équations dites cartésiennes d'ensembles de points
Par exemple tu peux prendre le repère) et alors :
et alors :
- le point A a pour coordonnées ( 0,0 )
- le point B a pour coordonnées ( 1,0 )
- le point C a pour coordonnées ( 1,1 )
et le point D a pour coordonnées ( 0,1 )
ps)
Il est très facile de "convertir" l'équation (produit scalaire)
(produit scalaire)
Une des méthodes est de se placer dans un repère orthonormé de
et de travailler avec les coordonnées des points et les équations dites cartésiennes d'ensembles de points
Par exemple tu peux prendre le repère
- le point A a pour coordonnées ( 0,0 )
- le point B a pour coordonnées ( 1,0 )
- le point C a pour coordonnées ( 1,1 )
et le point D a pour coordonnées ( 0,1 )
ps)
Il est très facile de "convertir" l'équation
capitaine nuggets a écrit:Attention !
Le produit scalaire n'est pas, comme on pourrait le penser, un produit de vecteur.
On a.
Pour trouver cette ensemble, on va faire intervenir le point, projeté orthogonal de
sur
.
Tu peux maintenant faire quelque chose :++:
@capitaine nuggets
En effet,si H est le projeté orthogonal de M sur la droite (AB) donc : AB.AM = AB.AH = 2 ..
ptitnoir a écrit:@Rimchi
Une des méthodes est de se placer dans un repère orthonormé de(plan euclidien)
et de travailler avec les coordonnées des points et les équations dites cartésiennes d'ensembles de points
Par exemple tu peux prendre le repèreet alors :
- le point A a pour coordonnées ( 0,0 )
- le point B a pour coordonnées ( 1,0 )
- le point C a pour coordonnées ( 1,1 )
et le point D a pour coordonnées ( 0,1 )
ps)
Il est très facile de "convertir" l'équation(produit scalaire)
@Ptitnoir
Donc AB ( 1,0) et AM ( x(M) - 0, y(M) - 0)
Alors AB.AM = 2 ( x(M)-0)* 1 + (y(M)-0 * 0) = 2
x(M) = 2
Donc M appartient à la droite x=2 ?
Rimchi a écrit:@Ptitnoir
Donc AB ( 1,0) et AM ( x(M) - 0, y(M) - 0)
Alors AB.AM = 2 ( x(M)-0)* 1 + (y(M)-0 * 0) = 2
x(M) = 2
Donc M appartient à la droite x=2 ?
Non.
Il y a une coquille :
ABCD est un carré de côté 2 donc il faut prendre :
A(0,0) ; B(2,0) ; C(2,2) et D(0,2).
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Rimchi a écrit:Je n'ai pas vraiment compris, on a pris quel repère?
Le problème avec le repère de ptitnoir c'est que le carré formé par les points A,B,C et D ne forme plus un carré de côté 2 comme dit dans l'énoncé, mais un carré de côté 1 !
C'est pour ça que je préférais privilégier un raisonnement vectoriel à un raisonnement analytique.
D'autant plus, que le raisonnement, me paraît plus court...
Rimchi a écrit:En effet,si H est le projeté orthogonal de M sur la droite (AB) donc : AB.AM = AB.AH = 2
Ca peut-être intéressant, précise-moi les vecteur et les longueurs stp
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Le problème avec le repère de ptitnoir c'est que le carré formé par les points A,B,C et D ne forme plus un carré de côté 2 comme dit dans l'énoncé, mais un carré de côté 1 !
C'est pour ça que je préférais privilégier un raisonnement vectoriel à un raisonnement analytique.
Ca peut-être intéressant, précise-moi les vecteur et les longueurs stp
D'accord A(0,0) ; B(2,0) ; C(2,2) et D(0,2).
AB.AM=AH.AB (tout en vecteurs) = AH.AB ( longeurs ) = 2
les coordonées de AB (vecteur) sont (2,0) donc AB ( longeur) =
et les coordonnées de AH aucune idée..
Mettons les coordonnées de côté : on ne s'en servira pas.
Si je réécris ce que tu as mis, on a ça :
 ?
?
N'hésite pas à reprendre mon post pour écrire de belle formules afin de lever toute ambiguïté :++:
Rimchi a écrit:AB.AM=AH.AB (tout en vecteurs) = AH.AB ( longeurs ) = 2
Si je réécris ce que tu as mis, on a ça :
N'hésite pas à reprendre mon post pour écrire de belle formules afin de lever toute ambiguïté :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Mettons les coordonnées de côté : on ne s'en servira pas.
Si je réécris ce que tu as mis, on a ça :?
Oui c'est bien ça. Mais je crois qu'il faut faire comme tout à l'heure:
AH ( x(H) - 0, y(H)- 0 ) et AB (2,0)
AH.AB =2 (x(H)-0)*2 + ( y(H) -0)*0 = 2
x(H) = 1
donc M appartient à la droite x=1 ...
capitaine nuggets a écrit:Mettons les coordonnées de côté : on ne s'en servira pas.
Si je réécris ce que tu as mis, on a ça :?
N'hésite pas à reprendre mon post pour écrire de belle formules afin de lever toute ambiguïté :++:
Oui c'est bien ça. Mais je crois qu'il faut faire comme tout à l'heure:
AH ( x(H) - 0, y(H)- 0 ) et AB (2,0)
AH.AB(vecteurs) = 2 (x(H)-0)*2 + ( y(H) -0)*0 = 2
x(H) = 1
donc M appartient à la droite x=1 ...
Rimchi a écrit:Oui c'est bien ça. Mais je crois qu'il faut faire comme tout à l'heure:
AH ( x(H) - 0, y(H)- 0 ) et AB (2,0)
AH.AB =2 (x(H)-0)*2 + ( y(H) -0)*0 = 2
x(H) = 1
donc M appartient à la droite x=1 ...
non, tu vas voir que ça n'est pas la peine.
D'ailleurs, je te ferais remarque que c'est l'inverse :
On va y aller successivement, mais le plus dur est fait :++:
Dans un premier temps, je voudrais que tu me dises pourquoi
Puis dans un second temps, pourquoi
Pour résumer :
Or
Connaissant la position de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:non, tu vas voir que ça n'est pas la peine.
D'ailleurs, je te ferais remarque que c'est l'inverse :.
On va y aller successivement, mais le plus dur est fait :++:
Dans un premier temps, je voudrais que tu me dises pourquoi?
Puis dans un second temps, pourquoi?
Pour résumer :équivaut à
avec
le projeté orthogonal de
sur
.
Ordonc tu en déduis
.
Connaissant la position desur
et le fait qu'il s'agisse du projeté orthogonal de
sur
, c'est fini !
1) AB.AM =AH.AB (vecteurs) tout ce que je sais c'est que c'est à partir la propriété du projeté
orthogonal..
2) AH.AB(vecteurs) = AH.AB.cos 0 = AH.AB
Ah..que suis-je bête. On a AH.AB=2 (longeurs) donc AH= 2/AB = 1
Ca me convient.
Tu sais que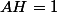 ,
, ) et
et  est le projeté orthogonal de
est le projeté orthogonal de  sur
sur ) donc tu en déduis l'ensemble
donc tu en déduis l'ensemble  .
.
Tu sais que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Rimchi a écrit:Puisque AMB est un triangle rectangle et AH=BH=1 ,c'est un cercle de rayon AH=1 et diamètre AB=2?
Non.
Déjà, si
C'est donc sa médiatrice.
(En effet, quel que soit
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
en fait si on a :
c'est surtout parce que :
: 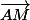 et
et  sont de même sens.
sont de même sens.
capitaine nuggets a écrit:.
c'est surtout parce que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
