Produit scalaire plan

[Françoisdesantilles]

Bonjour,
j'ai essayé de faire cet exo,
mais je voulais savoir si mes réponses sont bonnes svp?
https://ibb.co/SrC3CbW
a) (projete')
b) Soit le projeté orthogonal de sur .
.
c)
d) projeté orthogonal de sur

e)

f)

[vam]

Bonjour

a) ton résultat voudrait dire que les vecteurs sont orthogonaux (puisque aucun n'est nul), et ce n'est manifestement pas le cas.
J'aurais volontiers remplacé par
Je te laisse terminer.

[Françoisdesantilles]

Merci j'ai trouvé -AB²+1/2BA² = -3AB²/2 (de mémoire) , sauf erreur .
J'ai utilisé un projeté orhtogonale

[stummel]

Un produit scalaire ne peut être nul que si l'un des vecteur est nul ou si les deux vecteurs sont orthogonaux.
Quelle que soit la question, ce n'est jamais le cas : tu ne devrais donc jamais trouver 0 comme résultat.

En revanche, ton idée d'utiliser des projections orthogonale est intéressante mais il ne faut pas en oublier la moititée. Je prends uniquement la question a et te laisse faire les suivantes, qui sont un peu sur le même modèle.
Il y a deux manières de faire :
La première, la plus naturelle consiste à considérer le point H comme le projeté de E sur la drroite (AB).
On a donc :

D'où :

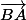
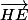
Comme : et sont orthogonaux leur produit scalaire est nul.

Il reste :

Et comme

Au final :

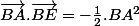
Deuxième manière, désigner par H comme le projeté de E sur (BC).
On a donc :

D'où :

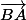
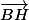
Cette fois ci ce sont et qui sont orthogonaux ; leur produit scalaire est nul.

Il reste :

Et comme

Au final :

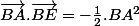
Ce qui donne heureusement le même résultat.