[B]produit scalaire, et orthogonalité[/B]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
ludo74
- Membre Relatif
- Messages: 119
- Enregistré le: 04 Oct 2006, 16:50
-
 par ludo74 » 24 Jan 2007, 11:33
par ludo74 » 24 Jan 2007, 11:33
Bonjour je suis en première S et j'ai un problème à résoudre grâce aux produits scalaires et au théorème de l'orthogonalité, j'ai réussi le 1) qui est très simple mais je bute sur le 2) si quelqun pouvait me donner un coup de main il me renderait un tres grand service.
J'ai inclus un schema de la situation
merci d'avance
L.
Dans le plan, ABC et ADE sont des triangles rectangles isocèles directs en A et I est le milieu du segment [DC].

1)Démontrer que : vecteur AD + vecteur AC= 2 vecteurs AI
2)Démontrer que les droites (AI) et (BE) sont perpendiculaires.
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 24 Jan 2007, 11:39
par anima » 24 Jan 2007, 11:39
ludo74 a écrit:Bonjour je suis en première S et j'ai un problème à résoudre grâce aux produits scalaires et au théorème de l'orthogonalité, j'ai réussi le 1) qui est très simple mais je bute sur le 2) si quelqun pouvait me donner un coup de main il me renderait un tres grand service.
J'ai inclus un schema de la situation
merci d'avance
L.
Dans le plan, ABC et ADE sont des triangles rectangles isocèles directs en A et I est le milieu du segment [DC].

1)Démontrer que : vecteur AD + vecteur AC= 2 vecteurs AI
2)Démontrer que les droites (AI) et (BE) sont perpendiculaires.
AD+AC = 2AI
BE = BA+AE
Fais ensuite des égalités avec les vecteurs que tu connais, en utilisant Chasles. A la fin, tu auras deux vecteurs que tu pourras faire en scalaire (u.v = UVcos(U,V)) :zen:
-
ludo74
- Membre Relatif
- Messages: 119
- Enregistré le: 04 Oct 2006, 16:50
-
 par ludo74 » 24 Jan 2007, 11:50
par ludo74 » 24 Jan 2007, 11:50
je ne vois pas ce que tu veux dire quand tu dis faire les égalités, je fais les égalités entre quels vecteurs et pour obtenir quoi??
De plus je ne comprends pas comment faire (U.V cos(u,v)) puisque je n'ai pas de longueurs et je n'ai pas d'angles.
Merci de m'avoir aider
ludovic
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 24 Jan 2007, 12:02
par annick » 24 Jan 2007, 12:02
Bonjour,
Pour la première question, pense à la relation de Chasles en introduisant I dans AD et AC
-
ludo74
- Membre Relatif
- Messages: 119
- Enregistré le: 04 Oct 2006, 16:50
-
 par ludo74 » 24 Jan 2007, 12:57
par ludo74 » 24 Jan 2007, 12:57
oui pour cette question j'avais compris comment faire mais ce n'est pas le cas de la seconde
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 24 Jan 2007, 13:20
par anima » 24 Jan 2007, 13:20
ludo74 a écrit:oui pour cette question j'avais compris comment faire mais ce n'est pas le cas de la seconde
Tu peux tenter d'introduire 2 vecteurs dont tu connais l'orthogonalité par rapport à AD et AE...
-
ludo74
- Membre Relatif
- Messages: 119
- Enregistré le: 04 Oct 2006, 16:50
-
 par ludo74 » 24 Jan 2007, 15:53
par ludo74 » 24 Jan 2007, 15:53
je ne comprends pas parce que il n' y a pas de vecteur orthogonal à AE ou à AD
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 24 Jan 2007, 15:57
par anima » 24 Jan 2007, 15:57
ludo74 a écrit:je ne comprends pas parce que il n' y a pas de vecteur orthogonal à AE ou à AD
Ahem.
BE=BA+AE
vecteur AD + vecteur AC= 2 vecteurs AI
Or, BA orthogonal à AC
et AE orthogonal à AD
Résultat: 2 vecteurs étant une somme parfaite de vecteurs orthogonaux deux à deux ne peut être qu'orthogonaux
-
ludo74
- Membre Relatif
- Messages: 119
- Enregistré le: 04 Oct 2006, 16:50
-
 par ludo74 » 24 Jan 2007, 16:05
par ludo74 » 24 Jan 2007, 16:05
je crois que j'ai compris la demonstration le probleme c'est que je n'ai pas vu de telle fromule dans mon cours aurait tu un moyen d'arriver à ce résultat avec les scalaires??
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 24 Jan 2007, 16:38
par anima » 24 Jan 2007, 16:38
ludo74 a écrit:je crois que j'ai compris la demonstration le probleme c'est que je n'ai pas vu de telle fromule dans mon cours aurait tu un moyen d'arriver à ce résultat avec les scalaires??
Oui, bien entendu.
AD+AC = 2AI
BE = BA+AE
On va dire que si AI est orthogonal à BE, alors 2AI l'est aussi (la norme n'a aucune influence sur l'angle)


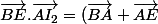.(\vec{AD}+\vec{AC}))
Un produit scalaire est-il distributif? oui
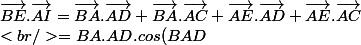 + 0 + 0 + AE.AC.cos(CAE) \\<br />= BA.AD(cos(BAD) + cos(CAE)) \\<br />= 0)
Du moins, si mes calculs sont justes. Refais la démonstration en tenant compte du 2AI, ca marchera bien
-
ludo74
- Membre Relatif
- Messages: 119
- Enregistré le: 04 Oct 2006, 16:50
-
 par ludo74 » 24 Jan 2007, 16:55
par ludo74 » 24 Jan 2007, 16:55
je ne comprends la premiere ligne AI(2)=AI/2=AD+AC pourrais tu me la réexpliquer
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 24 Jan 2007, 18:25
par anima » 24 Jan 2007, 18:25
ludo74 a écrit:je ne comprends la premiere ligne AI(2)=AI/2=AD+AC pourrais tu me la réexpliquer
J'ai juste posé que 2AI = AI(2) pour simplifier les calculs :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités

