Produit scalaire et ensemble de points
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mickaa_
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Mai 2010, 13:26
-
 par mickaa_ » 25 Mai 2010, 16:41
par mickaa_ » 25 Mai 2010, 16:41
Bonjour, j'aurais besoin d'un peu d'aide pour un exercice svp. Merci d'avance
Soit A et B deux points du plan tels que AB = 10.
I est le milieu de [AB] et M est un point quelconque du plan.
Tout d'abord, j'ai démontrer que produit scalaire MA.MB = MI²-(AB)²/4
Et après je dois déterminer l'ensemble E1 des points M du plan tels que MA.MB = 6
Donc j'ai fais MI² - IA² = 6
L'ensemble est un cercle ?
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 25 Mai 2010, 16:55
par gigamesh » 25 Mai 2010, 16:55
Bonjour,
IA c'est la moitié de AB vu que I est le milieu de [AB]
donc on a les équivalences
MI²-IA²=6
MI²=6+5²=31
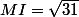
Je dirais que l'ensemble des points situés à une certaine distance de I,
ça ressemble méchamment à un cercle, ouais.
-
mickaa_
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Mai 2010, 13:26
-
 par mickaa_ » 25 Mai 2010, 17:05
par mickaa_ » 25 Mai 2010, 17:05
Merci :happy2:
Par contre est ce que vous pourriez me donner une piste pour la suite svp. Pasque je ne sais pas comment m'y prendre.
Je dois démontrer que MA² - MB² = 2AB.IM = 2AB.IH où H est le projeté orthigonal de M sur (AB)

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 25 Mai 2010, 17:50
par Ericovitchi » 25 Mai 2010, 17:50
oui tu écris
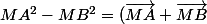.(\vec{MA}-\vec{MB})=(\vec{MI}+\vec{IA}+\vec{MI}+ \vec{IB}).\vec{BA}=2\vec{MI}.\vec{BA}=2\vec{AB}. \vec{IM}=2\vec{AB}(\vec{IH}+\vec{HM})=2\vec{AB}. \vec{IH})
-
mickaa_
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Mai 2010, 13:26
-
 par mickaa_ » 27 Mai 2010, 15:16
par mickaa_ » 27 Mai 2010, 15:16
Merci. Mais je ne comprends pas cette étape :
Ericovitchi a écrit:.(\vec{MA}-\vec{MB})=(\vec{MI}+\vec{IA}+\vec{MI}+ \vec{IB}).\vec{BA)
Pourriez vous m'expliquer svp ?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 27 Mai 2010, 15:24
par Finrod » 27 Mai 2010, 15:24
Il faut appliquer trois fois Chasles.
Pour découper le premier MA en passant par I.
Le premier MB en passant aussi par I.
et pour le membre de gauche on reconnait BM +MA.
-
mickaa_
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Mai 2010, 13:26
-
 par mickaa_ » 27 Mai 2010, 15:34
par mickaa_ » 27 Mai 2010, 15:34
Je comprends mieux
Merci à tous :we:
-
mickaa_
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Mai 2010, 13:26
-
 par mickaa_ » 27 Mai 2010, 15:37
par mickaa_ » 27 Mai 2010, 15:37
A la question suivante, je dois déterminer l'ensemble des points M du plan tels que MA² - MB² = 40
Je pense qu'il faut utiliser la question précèdente. Mais comment trouver l'ensemble ? Je ne vois pas comment faire.
Peut etre utiliser 2AB.IH ?
-
mickaa_
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Mai 2010, 13:26
-
 par mickaa_ » 27 Mai 2010, 16:41
par mickaa_ » 27 Mai 2010, 16:41
Est ce que quelqu'un pourrait m'aider à trouver l'ensemble des points M du plan tels que MA² - MB² = 40 svp. Merci d'avance

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Mai 2010, 21:25
par Ericovitchi » 27 Mai 2010, 21:25
Ben oui, 2AB.IH=40 tout est constant sauf H donc H est fixe et donc M se balade sur la droite perpendiculaire au point H
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
