Produit scalair et projetes orthogonaux
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Krys933
- Membre Relatif
- Messages: 410
- Enregistré le: 27 Oct 2006, 18:46
-
 par Krys933 » 19 Mar 2007, 23:23
par Krys933 » 19 Mar 2007, 23:23
Bonsoir à tous , je cale sur cette exo, pourriez vous me dire COMMENT le faire (le resultat n'est pas ce qui m'interesse je voudrais savoir comment faire)
ABC est un triangle rectangle en A
On designe par A' le milieu de [BC] et par H le projeté orthogonal de A sur (BC).
Le point H se projette orthogonalement en I sur (AB) et en J sur (AC)
Montrer que les droites AA') et (IJ) sont orthogonales.
Merci d'avance à tous
-
armor92
- Membre Relatif
- Messages: 262
- Enregistré le: 27 Déc 2006, 21:10
-
 par armor92 » 20 Mar 2007, 06:51
par armor92 » 20 Mar 2007, 06:51
Bonjour,
On prouve que le produit scalaire
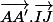
est nul.
A' est le milieu de BC, donc on peut écrire la relation :
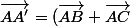/2)
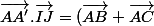.\vec{IJ}/2)
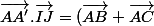.(\vec{IH}+\vec{HJ})/2)
On développe :
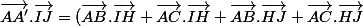/2)
Pour des raisons d'orthogonalité :
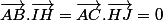
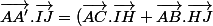/2)
On écrit
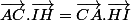
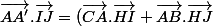/2)
On rajoute

et

qui sont nuls
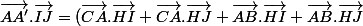/2)
On factorise :
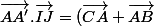.(\vec{HI}+\vec{HJ})/2)
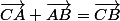
et
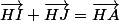
car AIHJ rectangle
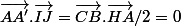
car BC ortogonal à HA
-
Krys933
- Membre Relatif
- Messages: 410
- Enregistré le: 27 Oct 2006, 18:46
-
 par Krys933 » 20 Mar 2007, 11:20
par Krys933 » 20 Mar 2007, 11:20
je comprend jusqu'à ta ligne
\vec{AA'}.\vec{IJ} = (\vec{AC}.\vec{IH}+\vec{AB}.\vec{HJ})/2
moi je trouve AA'. IJ = (AB.IJ + AC.IH) / 2 (le tout en vecteur)
comment explique tu que tu trouve AC.HJ ??
-
armor92
- Membre Relatif
- Messages: 262
- Enregistré le: 27 Déc 2006, 21:10
-
 par armor92 » 20 Mar 2007, 18:38
par armor92 » 20 Mar 2007, 18:38
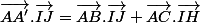
D'accord avec toi
Mais on peut développer
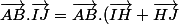 = \vec{AB}.\vec{IH} + \vec{AB}.\vec{HJ})
Mais
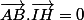
car AB orthogonal à IH
-
Krys933
- Membre Relatif
- Messages: 410
- Enregistré le: 27 Oct 2006, 18:46
-
 par Krys933 » 20 Mar 2007, 20:00
par Krys933 » 20 Mar 2007, 20:00
mais une question : à chaque fois c toute l'expressioon qui est divisé par deux ou juste une partie ?,
-
armor92
- Membre Relatif
- Messages: 262
- Enregistré le: 27 Déc 2006, 21:10
-
 par armor92 » 20 Mar 2007, 20:03
par armor92 » 20 Mar 2007, 20:03
C'est toute l'expression
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
