Problèmes logarithmiques aide !

[Sharer2006]

Bonjour, voilà je fais des exercices afin de me remettre à niveau mais j'ai des soucis pour résoudre un problème logarithmiques , je n'arrive pas à mettre la photo donc je vous met le lien ci dessous , qui se trouve a la page 91 à gauche , ce sont les exercices de tremblements de terre ! J'espere que vous pourriez m'aider a me donner les réponses ! merci

http://issuu.com/deboeckeducation/docs/cqfd66_complet

[Lamaths]

Pour quelles questions as-tu des difficultés ? As-tu fais les premières questions ?

Si ce n'est pas le cas, pour la (a) par exemple, tu as , et connaissant M, tu veux exprimer E.
Tu dois te débarrasser du "log" pour n'avoir que E du côté gauche de l'égalité. Quelle fonction connais-tu qui te permettrait de le faire ?

[Sharer2006]

Pour quelles questions as-tu des difficultés ? As-tu fais les premières questions ?

Si ce n'est pas le cas, pour la (a) par exemple, tu as , et connaissant M, tu veux exprimer E.
Tu dois te débarrasser du "log" pour n'avoir que E du côté gauche de l'égalité. Quelle fonction connais-tu qui te permettrait de le faire ?

Bonjour , merci pour la réponse , en réaliter pour la a) je l'avais déjà , mais ce sont les autres que je n'y arrive vraiment pas... je ne comprend pas et j'aimerai disons avoir un coup de main pour les réponses ! Ca serait très gentil merci

[Lamaths]

Ok, donc pour la (b) : à la question (a) tu as fait un tableau avec M et E.
Reste à placer ça dans un graphique : horizontalement tu gradues comme d'habitude et tu mets la magnitude, et verticalement ce sera logarithmique, c'est-à-dire que si tu prends 1cm pour aller de 0 à 10, tu prendras de nouveau 1cm pour aller de 10 à 100, puis 1 cm pour aller de 100 à 1000. (En gros un cm en plus correspond à multiplier par 10).
Ensuite tu places tes points dans ce graphique, et si tout va bien, tu devrais avoir une droite.

Pour la (c), il faut traduire la phrase mathématiquement.
ça te dit que si tu passes de M à M+2, alors E passe à 1000E.
En d'autres termes ayant log(E)=4.8+1.5M et log(E')=4.8+1.5M', tu sais que E'=1000E, alors combien vaut M'-M ?
Calcule log(E')-log(E) et essaye d'exprimer M'-M (l'énoncé te dit que M'-M vaut 2).

La (d) ressemble à la (c). Sauf que cette fois on te donne M'-M, et il faut que tu trouves E'/E

[Sharer2006]

Ok, donc pour la (b) : à la question (a) tu as fait un tableau avec M et E.
Reste à placer ça dans un graphique : horizontalement tu gradues comme d'habitude et tu mets la magnitude, et verticalement ce sera logarithmique, c'est-à-dire que si tu prends 1cm pour aller de 0 à 10, tu prendras de nouveau 1cm pour aller de 10 à 100, puis 1 cm pour aller de 100 à 1000. (En gros un cm en plus correspond à multiplier par 10).
Ensuite tu places tes points dans ce graphique, et si tout va bien, tu devrais avoir une droite.

Pour la (c), il faut traduire la phrase mathématiquement.
ça te dit que si tu passes de M à M+2, alors E passe à 1000E.
En d'autres termes ayant log(E)=4.8+1.5M et log(E')=4.8+1.5M', tu sais que E'=1000E, alors combien vaut M'-M ?
Calcule log(E')-log(E) et essaye d'exprimer M'-M (l'énoncé te dit que M'-M vaut 2).

La (d) ressemble à la (c). Sauf que cette fois on te donne M'-M, et il faut que tu trouves E'/E

Tu peux me montrer ce que tu as pour la C) D) E) ? pour avoir le correctif ?
merci

[Lamaths]

Je peux détailler la réponse de la question c.
Tu as log(E) = 4.8+1.5M, log(E') = 4.8+1.5M', et E'=1000E, tu cherches M'-M
log(E')-log(E)= 4.8+1.5M' -(4.8+1.5M) = 1.5(M'-M)
Or log(E')-log(E)= log(E'/E)= log(1000) (car E'=1000E)

Donc 1.5(M'-M)= log(1000)=3
M'-M = 3/1.5 = 2.

Donc, si l'énergie sismique est 1000 fois plus importante (E'=1000E), alors la magnitude s'élève de 2 degrés (M'= M+2).

Je peux aussi te donner les résultats numériques du (d) et (e), demande moi plus de détails si tu n'y arrives pas ;)
Pour une augmentation de magnitude de 0.2, l'énergie est multipliée par 2 (en gros), et pour l'autre, l’énergie est multipliée par 31.6

Et la consommation de la Belgique revient à un séisme d'amplitude 8.7.
(tous les chiffres sont arrondis)

[Sharer2006]

Merci bien , ça m'a bien aider je vois à peu près ! Maintenant j'ai un autre soucis ! Je dois déterminer le domaine de la fonction :

a)Log ( 1 )
------------
x² - 6x + 8

et je dois résoudre :

b) 3 * x+1 * + 3 * 2x+1* - 3*x+1* - 3 *2x+2* + 6 = 0

( CE QUI EST ENTRE * * C'EST EN REALITER MIS EN EXPOSANT MAIS COMME LE CLAVIER ORDINATEUR NE PERMET PAS DE LE METTRE JE L'AI REMIT COMME CA)

[Lamaths]

Pour la question a), ta fonction c'est ? ... ça me gène un peu parce que log(1) = 0... et étudier le domaine de définition de la fonction nulle, ce n'est pas très intéressant.

De manière assez générale quand même, quand tu as quelque chose du type , tu dois chercher les x tels que g(x)=0.
Ces points sont des valeurs interdites (car il est interdit de diviser par 0).
Dans ton cas, tu dois chercher les racines de x²-6x+8 pour les enlever du domaine de définition ... par contre, ça dépend aussi de ce qu'il y a en haut. Par exemple, si on met au numérateur log(x) à la place de log(1), il faut se souvenir que log(x) n'est définie que pour les x positifs. (Donc les x négatifs ne ferait pas partie du domaine de définition)


Pour le b), tu as (si je ne me trompe pas) , ça s'écrit aussi , car 2 termes se simplifient, et j'ai fait passer le 6 de l'autre côté de l'égalité.
Essaie de mettre en facteur à gauche, et penser à la fonction ln qui permet de faire "descendre" les puissances. Car

[Sharer2006]

Pour la question a), ta fonction c'est ? ... ça me gène un peu parce que log(1) = 0... et étudier le domaine de définition de la fonction nulle, ce n'est pas très intéressant.

De manière assez générale quand même, quand tu as quelque chose du type , tu dois chercher les x tels que g(x)=0.
Ces points sont des valeurs interdites (car il est interdit de diviser par 0).
Dans ton cas, tu dois chercher les racines de x²-6x+8 pour les enlever du domaine de définition ... par contre, ça dépend aussi de ce qu'il y a en haut. Par exemple, si on met au numérateur log(x) à la place de log(1), il faut se souvenir que log(x) n'est définie que pour les x positifs. (Donc les x négatifs ne ferait pas partie du domaine de définition)


Pour le b), tu as (si je ne me trompe pas) , ça s'écrit aussi , car 2 termes se simplifient, et j'ai fait passer le 6 de l'autre côté de l'égalité.
Essaie de mettre en facteur à gauche, et penser à la fonction ln qui permet de faire "descendre" les puissances. Car

Non non je l'ai mal écrit c'est:
log.......... ( 1 )
........... -------
.......... x²-6x+8

j'ai pas tout compris le B) , c'est la réponse?

[Lamaths]

Ok, donc si je comprends bien la a- c'est ?
Pour le domaine de définition, tu dois vérifier deux choses :
1. Il faut enlever les x tels que , car il est interdit de diviser par 0
2. Il faut que , car on ne prends pas le log de nombre négatifs.
Donc l'exercice revient à une étude d'un polynôme de degré 2.


Pour le b-, je n'ai pas donné de réponses, juste des indications.
Tu es d'accord que , c'est exactement la même chose que d'écrire ?
Pour continuer je te donne trois étapes :
1. Fais passer le "6" de l'autre côté de l'égalité
2. Mets en facteur.
3. Applique la fonction "log" à ton égalité.

Si ça ne t'aide pas, je te donnerai plus d'indications :lol3:

[Sharer2006]

Ok, donc si je comprends bien la a- c'est ?
Pour le domaine de définition, tu dois vérifier deux choses :
1. Il faut enlever les x tels que , car il est interdit de diviser par 0
2. Il faut que , car on ne prends pas le log de nombre négatifs.
Donc l'exercice revient à une étude d'un polynôme de degré 2.


Pour le b-, je n'ai pas donné de réponses, juste des indications.
Tu es d'accord que , c'est exactement la même chose que d'écrire ?
Pour continuer je te donne trois étapes :
1. Fais passer le "6" de l'autre côté de l'égalité
2. Mets en facteur.
3. Applique la fonction "log" à ton égalité.

Si ça ne t'aide pas, je te donnerai plus d'indications :lol3:

( oui le calcul c'est bien ça ) Et bien pour t'avouer je voudrais voir les réponses si tu sais me les donner ainsi je peu regarder en même temps que les explications , si ça ne te dérange pas :p.. Et j'étais en train de me dire pour les questions sur le tremblement de terre , le dernier post que tu as fait donnais les réponses non ? Car en fait je suis un peu perdu entre les réponses , ou les détails que tu fais , j'ai du mal à m'y retrouver je mélange un peu tout en pensant que quand tu donnes quelques chose c'est la réponse ou presque .. Donc ,je me demandais si tu as l'occasion de me donner la réponse en même temps ? Comme ça je ne m'embrouille plus et je peu suivre les explications et voir la démarche correcte avec la réponse qui va avec?

merci :p :ptdr:

[Lamaths]

Désolé que ce soit pas très clair :/
Dans l'idéal, je préfère éviter de donner des solutions complètes, et je ne donne que des indications pour que tu puisses chercher un peu. Car c'est plus efficace de bloquer mais de réussir un problème seul que de lire une solution.

Pour le post tremblement de terre, je t'ai donné les valeurs numériques pour que tu puisses les comparer aux tiennes. Mais je ne te donnais pas le raisonnement pour les dernières questions. Or en mathématique, ce qui est important c'est le raisonnement, et non la valeur.

Si tu y tiens, je peux te faire un corrigé pour le premier exercice.


a-Domaine de définition de
1. Recherche des racines de , en appliquant la méthode pour les équations de degré 2.
a=1, b=-6 et c=8

Donc, on a deux racines et
Donc, on a deux valeurs interdites : 4 et 2.

2. Il faut que , pour ne pas prendre le log d'un nombre négatif.
ça revient à chercher où est-ce que est positif.
D'après le cours, pour un polynôme du second degré, il est du signe de a en dehors des racines, et du signe de -a entre les racines.
Ici, ça veut dire que est strictement positif sur , et est négatif ou nul entre 4 et 2.

On veut juste les endroits où est strictement positif pour que soit positif (pour prendre le log d'un nombre positif) et que le dénominateur ne s'annule pas (pour ne pas diviser par 0), c'est à dire :

Conclusion : Le domaine de définition de est


Pour le deuxième exercice, j'aimerais plutôt que tu dises où est-ce que tu bloques, et ce que tu as déjà fait.

[Sharer2006]

bah disons que pour le deuxième exercice je l'ai fait , mais je suis pas certain d'avoir bon ,c'est pour ça que je préférais avoir ta réponse pour comparer pour si j'ai fait ca correctement

[Lamaths]

On aurait aussi pu le faire dans l'autre sens, tu me dis ce que tu as fait, et je vérifie si c'est bon.

Mais si tu veux, voici une correction possible de l'exercice 2 :

, donc .
En mettant 3^{2x+1} en facteur :
Donc
Donc (en divisant par 2)
En passant au log : , or
En simplifiant par log(3), ça fait 2x+1= 1, donc x=0

Ensuite, on peut vérifier que x=0 est bien solution car

Précise moi, s'il y a de choses que tu ne comprends pas, ou si tu ne trouves pas la même solution :lol3:

[Sharer2006]

heuuu oula j'ai un peu de mal à comprendre, ou est la solution?

Bah dire ce que j'ai ok ,mais j'arrive pas à faire les signes les exposants comme toi etc.. donc niveau gain de temps^^..
Parce que en attendant j'en fait d'autres j'ai une 30 aine d'autres à faire donc pdt que je regarde ce que tu as trouver je compare et je corrige si besoin mais entre temps je fais les autres quoi

[Lamaths]

Je vais essayer d'expliquer autrement
Tu as une équation où on te demande de trouver x.
Sur cette équation, j'ai fait un certain nombre de manipulations (que j'ai détaillé dans mon message précédent)
Et finalement, j'ai trouvé une seule solution qui est : x = 0 . C'est aussi ce que tu avais ?

Et pour les exposants, j'utilise un langage mathématique qui s'appelle .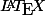
Pour l'utiliser, c'est quand tu tapes un message, tu as un bouton où il y a écrit TEX (tout à droit de la ligne où tu as les outils qui permettent de mettre en gras, en italique...etc)
Pour écrire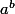 , le code à mettre entre des balises [ TEX] c'est a^{b}
C'est peut-être pas très clair, donc si tu veux plus d'explications, je te conseille ici : http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php

Mais c'est assez long d'écrire en Latex, tu gagnes pas de temps, mais c'est joli

J'espère que ça t'aide

[Sharer2006]

Oui ca m'aide pas mal , maintenant je vois , je m'étais tromper quelque part mais j'y arrivais !

[Sharer2006]

Maintenant un autre calcul tels que 16*-7.4*=8

( le * = x en exposant ) j'ai trouver 136 , peux tu me dire si ce que tu obtiens et cmt ?
et pour le calcul ici 2 * 2x * + 2 * x +1 * - 3 = 0

( ici par contre ce qu'il y a entre les * * sont mis en exposant ) , peux tu me dire ici ce que tu as ? car ma réponse n'est pas normale d'après moi

[Lamaths]

L'important en maths, c'est le raisonnement :lol3:
Je vais te donner la méthode pour résoudre le premier, et la valeur numérique du deuxième.


1. Pour le premier :

On remarque 16 = 4²
On récrit l'équation : .
On se souvient que
Donc
Ce qui signifie qu'écrire , c'est exactement pareil que d'écrire .

Pourquoi est-ce qu'on l'a écrit sous une autre forme ? -> Pour faire un changement de variable intéressant.
Tu poses
Comme ça, quand tu remplaces tous les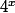 par des dans l'équation , tu obtient : .
Donc là, on est très content parce que c'est une équation du second degré, et on sait la résoudre.

Tu calcules le discriminant de .

On trouve deux racines et
Or, on se souvient qu'on a posé

Donc, ça veut dire que x est tel que :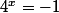 , ou .
Or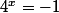 n'a pas de solution ! (Un nombre positif élevé à une puissance quelconque n'est jamais négatif !)
Donc, il reste à résoudre .
On passe au log : , donc

On trouve comme solution :

(Ceci dit... tu es sûr que l'équation de départ ce n'était pas plutôt : ? (il y a un + devant le 7 au lieu d'un moins). Je demande ça parce que avec un "+", on trouve des solutions plus simples )



2. Pour , la méthode est exactement la même.
Tu réécris l'équation sous la forme , et tu fais le changement de variable .
Après il faut finir les calculs, mais c'est la même méthode qu'avant.

Comme solution, tu vas trouver x=0

[Sharer2006]

haaaa d'accord merci.. Roh j'y étais pas trop j'avais fait autre chose... Merci de ton aide... purée dis, maintenant j'ai des problèmes à résoudre :

1) Si une population de bactéries triple toutes les 30min, combien aura-t-on de bactéries a^rès 10heures si la pop de bactéries initiale est de 5?

2)Les nénuphars du nil doublent leur nombre chaque jour? Un proprio en fait poser dans un lac. Cb de fleurs y aura-t-il après 15jours?

3)Une population de souris double en 3mois. Sachant qu'elle est actuellement de 20 000 unités et , qu'au départ il y avait 2 couples, depuis quand a t on créee cette colonie?

4) Dans une famille de lapins particulièrement prolifique, le nb d'individus double tous les 7 jours.
supposons que cette famille comprenne actuellement 100 lapins , cb y aura t'il de lapins dans 20 semaines ?

J'ai l'idée des réponses mais je veux vérifier , quel développement utilises tu pour arriver à la réponse?