Problème trapèzes

[LT76]

Voilà le problème j'espère que vous pourrez m'aider parce que je bloque dessus merci d'avance !

En Mésopotamie, les champs ont la forme de trapèzes.
Un arpenteur doit partager équitablement un champ entre deux frères : le champ est un trapèze de bases 7 et 17. Les
parts sont deux trapèzes. Trouver la largeur du milieu.

PS: normalement il y a un schéma avec mais je sais pas trop comment le mettre vu que je suis sur tel

[Lostounet]

PS: normalement il y a un schéma avec mais je sais pas trop comment le mettre vu que je suis sur tel

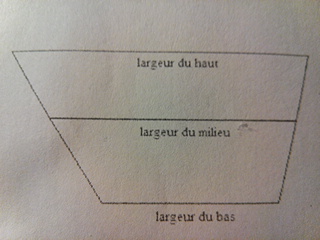
Ça te va?

[Pseuda]

Bonjour,

Il paraît évident que la largeur du milieu est la moyenne des 2, cela fait 12.

Petite indication : utiliser Thalès en complétant le trapèze par un parallélogramme dont les
côtés sont les droites parallèles.

[chan79]

Bonjour,

Il paraît évident que la largeur du milieu est la moyenne des 2, cela fait 12.
.

salut
Attention aux évidences.
On doit arriver à 13.

[zygomatique]

salut

le mot largeur n'a pas de sens ...

en géométrie on parle de longueur (de segment)

et le terme largeur s'utilise pour distinguer deux longueurs ... comme par exemple dans le cas conventionnel d'un quadrilatère ... où l'on note usuellement longueur et largeur deux côtés consécutifs d'un rectangle ...

et la longueur n'est pas plus longue que la largeur ...


pour en revenir au pb on veut donc deux parts de même aire pour satisfaire l'équité ...

avec le dessin de lostounet en notant a, b et c les trois bases (de la plus grande en haut à la plus petite en bas) et x et y les hauteurs des deux trapèzes il faut donc que :

et ensuite ...

[LT76]

On doit arriver à 13.

Mais comment tu fais pour trouver 13?

[chan79]

Le plus rapide: penser à l'agrandissement d'un triangle

[Pseuda]

Peux-tu expliciter ce que tu cherches par la largeur du milieu ?

S'agit-il de la longueur du segment qui passe par les milieux des côtés du trapèze (qui fait 12), ou de celui parallèle aux bases qui partage le trapèze en deux aires égales (je n'ai pas calculé) ?

[chan79]

salut
Le partage doit être équitable entre les deux frères. Donc, à priori, les aires des deux parts doivent être égales.

[LT76]

/Users/Louis/Downloads/IMG_20170730_152655.jpg
On cherche le côté marqué "?"

Et agrandir comme ça?

[LT76]

Ah mais oui du coup on voit pas l'image...

[chan79]

Tu agrandis le triangle vert, d'aire T.
Si tu multiplies par 17/7 tu as OCD.
Aire de OCD=T*(17/7)²
Si tu multiplies par k tu as OIJ
Aire de OIJ=T*k²
Aire de ABIJ= T*k²-T
Aire de ABCD=...
k doit être tel que
...
Miracle, T se simplifie!
Tu calcules k puis la distance cherchée.
17 et 7 n'ont pas été choisis au hasard.
Tu peux généraliser en remplaçant 7 et 17 par a et b.

[LT76]

Mais k il sort d'où?
Et Aire de OCD c'est aussi (h(7+17))/2 + T non? Comment tu arrives à Aire de OCD=T*(17/7)²

[chan79]

il s'agit justement de déterminer la bonne valeur de k (coef d'agrandissement)

[LT76]

Ah ok merci
Parce que on n'avait jamais fait de trucs comme ça en cours

[LT76]

Par contre je n'ai pas compris pourquoi le coefficient pour avoir Aire de OCD c'est 17/7 et pourquoi tu élèves au carré 17/7 après

[LT76]

Si tu pouvais m'expliquer stp

[chan79]

Lors d'un agrandissement (ou réduction) d'une figure, si les distances sont multipliées par k, l'aire est multipliée par k².

[LT76]

Ah bah oui jsuis bête
Merci

[LT76]

Bon le problème c'est que je vois toujours pas comment avancer dans le problème... Et j'ai trouvé (240T)/49 pour Aire de ABCD mais bon ça m'avance pas à grand chose