Problème tableau de signes :s

[eliwen]

Re-bonjour,

Je me permet de reposter un sujet concernant le petit c) de mon DM (le même que tout à l'heure).

Soit f(x)=x*e^-x
Pour tout réel x, prouver si f(x)== 0, soit -x >=-1, soit x== 1 et non [COLOR=Green]x =< 1..

Comment résoudre ce problème ? Merci de vos réponses en avance

[jlb]

Je me permet de reposter un sujet concernant le petit c) de mon DM (le même que tout à l'heure).

Soit f(x)=x*e^-x
Pour tout réel x, prouver si f(x)== 0, soit -x >=-1, soit [COLOR=Green]x=0 donc (e^(-x)) (1-x) >0 (e^u>0 pour u réel); la dérivée de f est donc positive pour x<1 elle est donc croissante sur cet intervalle.

[Carpate]

Re-bonjour,

Je me permet de reposter un sujet concernant le petit c) de mon DM (le même que tout à l'heure).

Soit f(x)=x*e^-x
Pour tout réel x, prouver si f(x)== 0, soit -x >=-1, soit x== 1 et non [COLOR=Green]x =< 1..

Comment résoudre ce problème ? Merci de vos réponses en avance

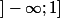
a pour dérivée qui est positive sur et négative ensuite donc maximum pour
donc proposition vraie
En fait partiellement vraie f(x) < 1 et non f(x) <= 1

[eliwen]

Merci beaucoup pour tout ! :))