Un Problème
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 02 Oct 2005, 16:47
par Anonyme » 02 Oct 2005, 16:47
Bonjour tout le monde!!
Je ne savais pas que se genre de forum existaient avant aujourd'hui.
Belle initiative !
Bon vous vous en doutez surement si je post ici, c'est bien pour un problem!( dm de math; Terminale S )
Le voici :
Soit f la fonction définie par : F(x)=1 + x/[V(x²+1)] (V racine carré^^)
1) étudier le sens de variation de f et établir son tablo de variation.
( pas de problem la, décroissante jusqu'a 1 puis croissante )
2)En utilisant la fonction

définie par

(x)= f(x)-x, prouver que l'équation f(x)=x admet une unique solution

,


[1;2]; donner une valeur approchée de

à 10-² prés
.
Bon la sa se corse un peu pour moi à la seconde quesiton .
Je pensais exprimer

(x) puis étudier sa limite en 0, mais sa ne me donne rien, d'autant plus qu'il me faut un encadrement de

dans [1;2]
Je vous demande de m'aider, mais plus qu'une solution, je voudrais avant tout comprendre.
Merci à tous.
-
Chimerade
- Membre Irrationnel
- Messages: 1472
- Enregistré le: 04 Juil 2005, 13:56
-
 par Chimerade » 02 Oct 2005, 17:00
par Chimerade » 02 Oct 2005, 17:00
destroyer a écrit:Bonjour tout le monde!!
Je ne savais pas que se genre de forum existaient avant aujourd'hui.
Belle initiative !
Bon vous vous en doutez surement si je post ici, c'est bien pour un problem!( dm de math; Terminale S )
Le voici :
.
Bon la sa se corse un peu pour moi à la seconde quesiton .
Je pensais exprimer

(x) puis étudier sa limite en 0, mais sa ne me donne rien, d'autant plus qu'il me faut un encadrement de

dans [1;2]
Je vous demande de m'aider, mais plus qu'une solution, je voudrais avant tout comprendre.
Merci à tous.
Je serais toi, je commencerais par étudier les variations de

, en étudiant sa dérivée. Ensuite, si par hasard la fonction est monotone entre 1 et 2, je calculerais

(1) et

(2), et avec de la chance, si les deux valeurs encadrent 0, je pourrais ainsi prouver qu'il y a une valeur de x telle que

(x)=0.
Je ne l'ai pas fait, mais essaie ça d'abord !
-
destroyer82
- Membre Naturel
- Messages: 38
- Enregistré le: 02 Oct 2005, 16:08
-
 par destroyer82 » 02 Oct 2005, 17:33
par destroyer82 » 02 Oct 2005, 17:33
Ok sa marche, mais comment fait on pour donner une valeur aproché à 10-2 pré? il ne faut tout de même pas utiliser la calculette?
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 02 Oct 2005, 17:38
par Galt » 02 Oct 2005, 17:38
Bonsoir
Si, justement, il faut la calulatrice
Il y a plusieurs méthodes, mais toutes emploient la calculette
Soit tu as un solveur, et no problem
Soit tu fais une table des valeurs de f(x)-x, en prenant un x mini de 1, et un pas de 0,1 (et un x maxi de 2, si c'est une Casio)
Au changement de signe, tu as un encadrement de ta valeur à 0,1 près
Tu recommence entre ces valeurs avec un pas de 0,01
Ca s'appelle une méthode de balayage
-
destroyer82
- Membre Naturel
- Messages: 38
- Enregistré le: 02 Oct 2005, 16:08
-
 par destroyer82 » 02 Oct 2005, 17:55
par destroyer82 » 02 Oct 2005, 17:55
Merci pour votre aide, mais je bloque ensuite à la question 3 de la suite de l'exercice que je vous ai précédament exposer...
Suite de l'exercice :
Soit g la fonction définie sur R par: g(x)=x+V(x²+1)
on désigne (C) la courbe représentative de g dans un repère orthonormal
1)a)etudier les limites de g en +linfini et -l'infini
b)Etudier le sens de variation de g
2)a)Prouver que la droite (D) d'équation y=2x est assymptote à (C), existe-t-il une autre assymptote?
b)Construire (C)
!!3)!! Soit (R) la courbe d'équation y²-2xy-1=0
Justifier que (R) est la réunion de la courbe (C) et d'une autre courbe (C'); en déduire la construction de (R)
Merci de votre future aide pour la question 3)
-
Chimerade
- Membre Irrationnel
- Messages: 1472
- Enregistré le: 04 Juil 2005, 13:56
-
 par Chimerade » 02 Oct 2005, 18:44
par Chimerade » 02 Oct 2005, 18:44
destroyer82 a écrit:y²-2xy-1=0
En général, tu es habitué à avoir une fonction du type y=f(x), n'est-ce pas ?
Effectivement, c'est pratique !
Alors, si tu considérais cette équation comme une équation du second degré en y, ne pourrais-tu pas exprimer y en fonction de x ?
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 02 Oct 2005, 18:44
par Galt » 02 Oct 2005, 18:44
Si tu considère ta courbe comme une équation du secon degré, que donne la résolution de y en fonction de x?
-
destroyer82
- Membre Naturel
- Messages: 38
- Enregistré le: 02 Oct 2005, 16:08
-
 par destroyer82 » 02 Oct 2005, 18:57
par destroyer82 » 02 Oct 2005, 18:57
(oui je suis généralement habitué à des équation de la forme y=f(x))
-j'ai bien essayé d'exprimer y en fonction de x, sans succé, je narrive pas à isoler y
- j'ai aussi essayé de décomposé y²-2xy-1=0 en la somme de 2 équation :
Y²=2 ou y=V2) et y=1/2x
ce qui donne y²=2 et 2xy=1
dc y²-2xy=2-1
y²-2xy-1=0
Mais je ne suis sur de rien, surtout pas si j'ai le droit de faire ce que je vient de faire, deplus comment faire le lien avec la courbe (C) de g(x)=x+V(x²+1)
-sinon je ne comprend pas t'es expliquation galt, désolé..
Que veut tu dire par "une équation du second degré en y"?
-je n'arrive pas à afficher ma courbe à partir de ma casio^^ est ce possible avec ce type d'équation?
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 02 Oct 2005, 21:30
par Galt » 02 Oct 2005, 21:30
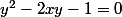
peut être considéré comme une équation où l'inconnue est y (et x est supposé connu). On la résout avec
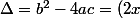^2+4)
-
destroyer82
- Membre Naturel
- Messages: 38
- Enregistré le: 02 Oct 2005, 16:08
-
 par destroyer82 » 04 Oct 2005, 18:40
par destroyer82 » 04 Oct 2005, 18:40
ok jusque la je te suis
j'arrive à Y=x-V(x²+1) ou Y=x+V(x²+1)
une de ces propositions définient donc (R) (?...)
-
Y=x+V(x²+1) ressemble à g(x)=x+V(x²+1) de courbe (C)
or il me faut justifier que la courbe (R) et la réunion de (C) et de (C')
(comment si il y a lieu d'être)
-
je remarque aussi que Y=x-V(x²+1) c'est Y=x+V(x²+1) -2x
Est ce que je peu en déduire que (R) et la réunion de (C) d'éq y=x+V(x²+1) et de (C') d'éq y=-2x
(Si oui comment éliminer la proposition Y=x+V(x²+1))
Merci galt
PS: comment fait tu galt pour afficher les équations avec des caractère spéciaux sur fond blanc ?
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 04 Oct 2005, 18:49
par Galt » 04 Oct 2005, 18:49
Non, tu as bien trouvé la première courbe
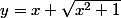
qui est la courbe de g. L'autre c'est la courbe d'équation
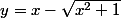
, qui est tout bêtement la courbe de la fonction f :

-
destroyer82
- Membre Naturel
- Messages: 38
- Enregistré le: 02 Oct 2005, 16:08
-
 par destroyer82 » 05 Oct 2005, 13:25
par destroyer82 » 05 Oct 2005, 13:25
oui, mais encore?
Comment est ce que je peut justifier que (R) est la réunion de (C) et (C')???
(réunino = somme non?)
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 05 Oct 2005, 14:30
par Galt » 05 Oct 2005, 14:30
Ben non, la réunion ce n'est pas la somme. La réunion de deuxn ensembles, c'est quand on prend ces deux ensembles pour en faire un seul.On recherche un ensemble de points, et les points correspondants sont soit sur une des courbes, soit sur l'autre. Ils sont bien sur la réunion des deux courbes.
Pour les équations, j'utilise le langage TEX, il y a la balise au dessus de la fenêtre de saisie; C'est assez difficile au début, par ex pour faire la racine de x carré plus , on tape \sqrt{x^2+}.
Pour voir comment ça marche, tu peux prendre des posts où il y en a et répondre en les citant, comme ça tu vois ce qui a été tapé. Il y a le bouton prévisualisation du message pour se corriger, et il y a le sujet "TEX disponible sur le forum" que tu peux lire.
-
destroyer82
- Membre Naturel
- Messages: 38
- Enregistré le: 02 Oct 2005, 16:08
-
 par destroyer82 » 05 Oct 2005, 15:21
par destroyer82 » 05 Oct 2005, 15:21
ok je te remercie galt
Désolé d'être aussi lourd( de mon ignorance^^) à poser autant de question, mais:
Comment tracer (R) dans ce cas, je ne vais quand même pas tracer la courbe d'équation y=x+V(x²+1) et la courbe d'équation y=x-V(x²+1) ???
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 05 Oct 2005, 16:29
par Galt » 05 Oct 2005, 16:29
Je ne vois guère ce que tu pourrais faire d'autre ...
-
destroyer82
- Membre Naturel
- Messages: 38
- Enregistré le: 02 Oct 2005, 16:08
-
 par destroyer82 » 05 Oct 2005, 16:39
par destroyer82 » 05 Oct 2005, 16:39
ok, je demande car je découvre, nous n'avons jamais rien fait de ce type la en classe, donc je suis incertain sur tout^^
Merci galt
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 05 Oct 2005, 17:26
par Galt » 05 Oct 2005, 17:26
En général, tu as de bonnes idées. AIe un peu plus confiance en toi. Il faut monter au filet et lâcher les coups.
A bientôt
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
définie par
(x)= f(x)-x, prouver que l'équation f(x)=x admet une unique solution
,

[1;2]; donner une valeur approchée de
à 10-² prés
