Problème N.C

[Fan-de-Perelman]

Bonsoir,

voici un exercice plus ou moins simple de nombres complexes :

soit z un élément de-{i}.On considère le nombre complexe :
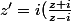1) montrez que
2)a- montrez que
b- en conclure l'ensemble de point M(z) sachant que
3)a- démontrez que pour tout z appartenant à -{i,-i}
b-EN CONCLURE L'ENSEMBLE DE POINT M(Z) SACHANT QUE

je bloque complètement à la dernière réponse ... Merci d'avance pour votre précieuse aide.

[manoa]

Hallo

Que veut dire z' R+ ?

[Fan-de-Perelman]

hello ,

et bien que le nombre z' soit un réel strictement positif

[manoa]

hello ,

et bien que le nombre z' soit un réel strictement positif

je veux dire en terme d'argument :lol5:

[Fan-de-Perelman]

que arg(z') équivaut à 0 modulo 2pi mais faut quand même avoir comme resultat l'argument de z . non?

[globule rouge]

Hallo

Que veut dire z' R+ ?

Un petit indice : en terme d'argument

Julie

Edit : désolée j'avais oublié d'actualiser :girl2:

[globule rouge]

que arg(z') équivaut à 0 modulo 2pi mais faut quand même avoir comme resultat l'argument de z . non?

Oui et bien arg((z+i)/(z-i))=-pi/2(mod 2pi) arg((z+i)/(z-i))=arg(-i)...

[manoa]

ce qui est demandé c'est l'ensemble des points z , donc trouver l'argument de z n'est pas obligatoire.

tu as donc



Si je pose A(-i) et B(i) , que peux tu déduire à propos de l'angle

[Fan-de-Perelman]

ce qui est demandé c'est l'ensemble des points z , donc trouver l'argument de z n'est pas obligatoire.

tu as donc



Si je pose A(-i) et B(i) , que peux tu déduire à propos de l'angle

que (AM) est perpendiculaire à (BM) et donc que l'ensemble de point est la mediatrice du segment [AB] ... j'ai mal refléchi sur ce coup là. Merci en tout cas.

Mais est-ce que la question 2)a- peut nous être utile ?

[chan79]

que (AM) est perpendiculaire à (BM) et donc que l'ensemble de point est la mediatrice du segment [AB] ... j'ai mal refléchi sur ce coup là. Merci en tout cas.

Mais est-ce que la question 2)a- peut nous être utile ?

On trouve que M appartient à un demi-cercle de diamètre [AB] , A et B exclus
Je trouve que ce problème se résout plus facilement en posant z=x+iy et en exprimant z' en fonction de x et y mais il faut suivre le texte...

[Fan-de-Perelman]

On trouve que M appartient à un demi-cercle de diamètre [AB] , A et B exclus
Je trouve que ce problème se résout plus facilement en posant z=x+iy et en exprimant z' en fonction de x et y mais il faut suivre le texte...

en effet, ce n'est pas la mediatrice

[Fan-de-Perelman]

comme suite de l'exercice on considère l'equation sachant que n est entier naturel et n>=2

(ne sachant pas ce qu'est X, à cause d'une défaillance de la photocopieuse :--: ... serait-ce i?)

a- démontrez que
b- en conclure que les images des solution de l'equation (E) sont linéaire
c- démontrez que les solutions de l'équation (E) s'écrivent :

pour l'instant je bloque en a et b ... (on peut sauter la question a vu qu'on a pas d'information sur X mais on peut repondre aux question b et c)

[manoa]

(ne sachant pas ce qu'est X, à cause d'une défaillance de la photocopieuse :--: ... serait-ce i?)

Je pense que le X est le signe ' , colle avec la première question , pour les autres questions , je pense qu'il y avais un truc pareil dans un de nos DS , je vais y pensé ..