Problème sur primitive

par **glanp** » 13 Déc 2009, 15:29

Bonjour,
je bloque sur un exercice de maths depuis ce matin et je post donc sur le forum pour avoir un peu d'aide ...

alors voila, je dois calculer une integrales a partir de cette fonction :
f(t)= 1/(1+t²)

Et j'ai enorment de mal a calculer F(t)
Merci d'avance

par **benekire2** » 13 Déc 2009, 15:41

Tu dois bien pouvoir arriver à la composée celle-ci :doh:

par **glanp** » 13 Déc 2009, 15:44

avec u=1 et v=1+t² ... mais il n'existe pas de formule ....

par **Ben314** » 13 Déc 2009, 16:19

Bonsoir,
Je ne sait pas à quel niveau tu est, mais une primitive de 1/(t²+1) est... arctan(t) c'est à dire la bijection réciproque de la fonction tangente.
Et il me semble que, si on ne le sait pas et qu'on a pas d'indic.... on l'invente assez difficilement....

par **glanp** » 13 Déc 2009, 16:29

Et bien je suis en Terminale S et ... on a jamais parlé de ça ...
j'ai trouvé pour F(t) =-2t/(1+t²)²
mais c'est probablement faux

par **Ben314** » 13 Déc 2009, 16:33

Est tu SÛR que la fonction dont tu doit trouver la primitive est

?

P.S. car moi, je suis sûr que dans ce cas tu ne peut pas au niveau term. inventer la primitive de cette fonction...

P.S.2 As tu vu les changement de variable dans les intégrales ?

par **glanp** » 13 Déc 2009, 16:36

et bien oui ... enfin on me demande calculer l'integrale de f(t), je passe donc par la primitive ...

par **Ben314** » 13 Déc 2009, 16:46

Si tu sait comment on dérive une bijection réciproque (voir à la limite en conaissant la façon de dériver une composée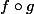

) tu peut vérifier que la dérivée de arctan(t) et 1/(1+t²) mais honnêtement, je vois pas comment tu peut "intuiter" un tel résultat sans indic. dans l'énoncé et sans l'avoir vu en cours....

par **Nightmare** » 13 Déc 2009, 16:58

L'énoncé ne parle nulle part de primitive mais d'intégrale. Je pense surtout que notre ami à a étudier la fonction

!

En l'occurrence montrer en dérivant que

là ou ça a du sens :happy3:

Problème sur primitive

Problème sur primitive

Qui est en ligne