Problème sur la distance de freinage

[miriam]

Bonsoir,


On considère un véhicule dont la distance de freinage sur route sèche (en mètres) est donnée par :
Ds(v) = 0.005v² + 0.27v -----) où v est exprimée en km.h-1

A/ quel panneau de limitation doit-on placer dans une rue où l’on souhaite que ce véhicule ait une distance d’arrêt inférieures à 15 m sur route sèche ?

B/ Sur route mouillée, la distance de freinage de ce véhicule est :
Dm(v) = 0.007v² + 0.27v


Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0.005v² + 0.27v - 15 = 0
V(0.005V + 0.27) – 15 = 0

Ds(v) = 0.007v² + 0.27v
15 = 0.007v² + 0.27v
0.007v² + 0.27v - 15 = 0
V(0.007V + 0.27) – 15 = 0

Est-ce que je suis sur la bonne voie ? par contre je suis coincée à ce niveau.

[jlb]

salut, tu peux relire ton exercice: ça parait bizarre de parler de distance d'arrêt et de distance de freinage pour désigner la même chose. I n'l y a pas dans l'énoncé un histoire de temps de réaction?

confirme moi cela et on poursuit avec le bon énoncé!

[mrif]

Bonsoir,


On considère un véhicule dont la distance de freinage sur route sèche (en mètres) est donnée par :
Ds(v) = 0.005v² + 0.27v -----) où v est exprimée en km.h-1

A/ quel panneau de limitation doit-on placer dans une rue où l’on souhaite que ce véhicule ait une distance d’arrêt inférieures à 15 m sur route sèche ?

B/ Sur route mouillée, la distance de freinage de ce véhicule est :
Dm(v) = 0.007v² + 0.27v


Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0.005v² + 0.27v - 15 = 0
V(0.005V + 0.27) – 15 = 0

Ds(v) = 0.007v² + 0.27v
15 = 0.007v² + 0.27v
0.007v² + 0.27v - 15 = 0
V(0.007V + 0.27) – 15 = 0

Est-ce que je suis sur la bonne voie ? par contre je suis coincée à ce niveau.

C'est presque ça:
Il faut exprimer que , cela te ramène à l'inéquetion: .

Et là, tu essaies de te souvenir de ce que tu as appris sur le signe d'un polynome du second degré.
("signe de a à l'exterieur des racines, signe de -a à l'interieur des racines", ça te dit quelque chose?

[miriam]

C'est presque ça:
Il faut exprimer que , cela te ramène à l'inéquetion: .

Et là, tu essaies de te souvenir de ce que tu as appris sur le signe d'un polynome du second degré.
("signe de a à l'exterieur des racines, signe de -a à l'interieur des racines", ça te dit quelque chose?

Bonsoir mrif,

je vous prie de m'en excuser, j'ai oublié de rajouter à la question

B/ Sur route mouillée, la distance de freinage de ce véhicule est :
Dm(v) = 0.007v² + 0.27v
A quelle distance de freinage sur route mouillée est elle 20% supérieure à celle sur route sèche ?


on m'a dit de chercher le discriminant :

Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0.005v² + 0.27v - 15 = 0
V(0.005V + 0.27) – 15 = 0
= (0.27)2 (4 × 0.005 × -15) = 0.0729 + 0.3 .
Le discriminant est égal à 0.3729.


j'ai remplacé 20% par 1.2 donc

Ds(v) = 0.007v² + 0.27v
1.2 = 0.007v² + 0.27v
0.007v² + 0.27v + 1.2 = 0
= (0.27)2 (4 × 0.007 × 1.2) = 0.0729 0.0336 .
Le discriminant est égal à 0.0393.


j'ai fait cela sans vraiment comprendre ce que je fais.

[mrif]

Pour le moment, essaie de te limiter à la première question.
Oui, pour résoudre l'inéquation citée dans mon précédent post, on doit résoudre l'équation , et pour cela on a besoin de connaitre son discriminant que tu as calculé.

Et maintenant il faut calculer les 2 racines:
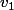et .

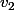Une fois que tu as trouvé ces racines, quelles sont les valeurs de v qui vérifient l'inéquation: ?

[miriam]

Pour le moment, essaie de te limiter à la première question.
Oui, pour résoudre l'inéquation citée dans mon précédent post, on doit résoudre l'équation , et pour cela on a besoin de connaitre son discriminant que tu as calculé.

Et maintenant il faut calculer les 2 racines:
et .

Une fois que tu as trouvé ces racines, quelles sont les valeurs de v qui vérifient l'inéquation: ?

Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0.005v² + 0.27v - 15 = 0
V(0.005V + 0.27) – 15 =
= (0.27)2 (4 × 0.005 × -15) = 0.0729 + 0.3 .
Le discriminant est égal à 0.3729.
L'équation admet 2 solutions réelles, car > 0

v1 = -27 - 3729
v2 = -27 + 3729

Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0.005v² + 0.27v - 15 = 0
= (0.27)2 (4 × 0.005 × -15) = 0.0729 + 0.3 .
Le discriminant est égal à 0.3729.
L'équation admet 2 solutions réelles, car > 0.

v1 = -27 - 3729
v2 = -27 + 3729


0.007v² + 0.27v + (-15 x 1.2 ) = 0
0.007v² + 0.27v -18 = 0
= (0.27)2 (4 × 0.007 × -18) = 0.0729 0.504 .
Le discriminant est égal à -0.5769

L'équation n'admet aucune solution réelle, car < 0.

v1 = -135 - 15x 641 / 7
v2 = -135 + 15x 641 / 7

[miriam]

Bonsoir,


Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0.005v² + 0.27v - 15 = 0
;) = (0.27)2 ;) (4 × 0.005 × -15) = 0.0729 + 0.3 .
Le discriminant est égal à 0.3729.
L'équation admet 2 solutions réelles, car ;) > 0.

v1 = -27 - ;)3729
v2 = -27 + ;)3729


0.007v² + 0.27v + (-15 x 1.2 ) = 0
0.007v² + 0.27v -18 = 0
;) = (0.27)2 ;) (4 × 0.007 × -18) = 0.0729 ;) 0.504 .
Le discriminant est égal à -0.5769

L'équation n'admet aucune solution réelle, car ;) < 0.

v1 = -135 - 15x ;)641 / 7
v2 = -135 + 15x ;)641 / 7


je vous remercie de m'indiquer la démarche à suivre.

[miriam]

Bonsoir,

0.005v² + 0.27v - 15 = 0
;) = (0.27)² ;) (4 × 0.005 × -15) = 0.0729 + 0.3 .
Le discriminant est égal à 0.3729.
L'équation admet 2 solutions réelles, car ;) > 0.

v1 = (-0,27 - ;)0,3729)/(2x0,005) = -88,07
v2 = (-0,27 + ;)0,3729)/(2x0,005) =34,07

S = ] 0 ; 34.07 ]

On doit placer un panneau limitant la vitesse à 30 km/h,

Je corrige sur ta réponse
0.007v² + 0.27v + (-15 x 1.2 ) = 0
0.007v² + 0.27v -18 = 0
;) = (0.27)² ;) (4 × 0.007 × (-18)) = 0.0729 ;) 0.504 .
Le discriminant est égal à 0.5769

L'équation admet deux solutions réelles, car ;) > 0.

v1 =( -0,27 - ;)0,5769) / (2x0,007) = -73,54
v2 =( -0,27 + ;)0,5769) / (2x0,007) = 34,97

S = ] 0 ; 34.07 ]

[Math3matiqu3]

Euh... 15 est en mètre , mais la vitesse est exprimée en km/h , ça gène pas ?