Bonjour ;
Soit i et j deux vecteurs de plan non colinéaires . Dans chacun des cas suivants , determiner , lorsqu'il existe ,le nombre réél k tel que v =k u
a) u = i + j et v = 2 i + 2 j
b) u = -1/2 i + 3 j et v = 2 i + 6 j
c) u = 4/5 i - 3/2 j et v = 2 i - 15/4 j
d) u = - 1/3 i + 9/4 j et v = 2/9 i - 3/2 j
e) u = -10 i - 3 j et v = - 2 i - 2/5 j
f) u = 2 i - 6/7 j et v = 7 i - 3 j
Je coule literalement sur cette exercice :briques: :mur: , je n'ai absolument rien compris , quelqu'un peut m'aider ? Je vous remercie d'avance
Probleme sur des vecteurs de plan non colinéaires
5 messages
- Page 1 sur 1
Bonsoir
Si on a et
et  ,
, =kx \vec i +ky \vec j)
donc si il existe un réel
si il existe un réel  tel que
tel que 
a)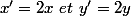 donc
donc 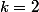 et
et 
b)
 soit
soit 
y=3, y'=6 donc y'=2y
On ne trouve pas le même nombre k pour les deux coordonnées donc il n'existe pas de nombre k tel que
Tu continues de la même manière, tu calcules . Si tu trouves le même nombre, il existe bien un réel k tel que
. Si tu trouves le même nombre, il existe bien un réel k tel que  . Si les quotients obtenus sont différents il n'existe pas de nombre k tel que
. Si les quotients obtenus sont différents il n'existe pas de nombre k tel que 
Si on a
donc
a)
b)
y=3, y'=6 donc y'=2y
On ne trouve pas le même nombre k pour les deux coordonnées donc il n'existe pas de nombre k tel que
Tu continues de la même manière, tu calcules
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
