Problème suite

[heroes]

Bonjour, voila je penche sur un problème depuis un petit moment, et je bloque... :help:

Enoncé :
On suppose que la population d'un pays est constante et égale à 120 millions d'habitants, dont 80millions en zone rurale et 40 millions en zone urbaine l'année notée "année zéro".

On suppose que chaque année, 10% de la population rurale part en ville et 5% de la population urbaine part à la campagne.

On note Rn et Un les effectifs en millions des ruraux et des citadins après n années. On a donc : R0=80 et U0=40



a) Que vaut Rn+Vn, pour tout n de N ?

Rn=80-8^n+2^n
Un=40+8^n-2^n

Rn+Vn=120, pour tout n de N

b) Calculer R1 et U1

R1=74
U1=46

c)Déterminer R(n+1) en fonction de Rn

Je n'y arrive pas...je ne vosi pas que faire...La suite n'étant ni arithmétique, ni géométrique :s

d) Démonter que les suite (Un-80) et (Rn-40) sont géométriques de raison 0,85, puis exprimer Rn et Un en fonction de n.

De même; bloquage complet...

Pourriez-vous m'aider, merci d'avance

[Flodelarab]

On suppose que chaque année, 10% de la population rurale part en ville et 5% de la population urbaine part à la campagne.

a) Que vaut Rn+Vn, pour tout n de N ?

Rn=80-8^n+2^n
Un=40+8^n-2^n

Tu crois vraiment ce que tu as écrit?
8^2=64
8^3=512

.... où est la justification ?

[nuage]

Salut,
je ne comprend pas ta justification de la question a.
On te demande juste de calculer Rn+Vn or apparemment il n'y a ni naissance ni mort juste une population qui se déplace. Qu'elle est la taille de cette population en fonction de Rn et Vn ? Ce qui permet de retrouver ta réponse sans calcul.

pour la question c je de demande si l'énoncé n'est pas :
[INDENT]calculer et 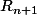en fonction de 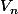et 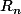[/INDENT]
Ce qui semble plus facile.

[heroes]

non, c'est effectivement stupide, mais je suis totalement largué sur cette exercice... :triste:

bon,

la réponse au a) est 120, vu que la population du pays est constante et égale à 120.

Pour le b),
R1=74 (80-10/100*80+5/100*40)
et U1=46 (40+10/100*80-5/100*40)

Pour déterminer R(n+1) en fonction de Rn, je ne vois pas comment faire vu que je ne vois pas si la suite est arithmétique ou géométrique. Enfin je pense qu'elle est géométrique, mais ce n'est pas très rigoureux de mettre :

R1=R0*q^(1-0)
74=80*q
q=74/80
q=0,925

D'ou : R(n+1)=Rn*0,925^n

Mais ca parait bizarre...et faux

Pourriez-vous m'aider :s

EDIT : non pour la c) l'énoncé est bien : Puis déterminer R(n+1) en fonction de Rn

[Flodelarab]

Pour moi, on a la matrice de tranformation.
la population l'année n

Et on a la formule: V(n+1)=M^nV(n)

Il est absurde de déterminer une population sans l'autre.

[heroes]

erf, sauf que je sort d'une 1ère S est que la matrice de transformation ne me parle absolument pas

[heroes]

hmmm j'ai peut etre quelque chose :

R1=V1+28
V1=V0+6
R1=V0+6+28
R1=V0+34

Or V0=Ro/2

D'ou R1=R0/2+34

On en conclue que : R(n+1)=Rn/2+34

[Flodelarab]

Moi j'ai enseigné ça à des 1ères ES.


Mais intuitivement, tu te rends bien compte que tu ne peux pas parler d'une population sans l'autre.

J'ajoute que, si tu calcules R2 et V2 par curiosité, tu vois bien que ni Rn, ni Un ne sont géométrique (pas la même raison pour passer de R0 à R1 que R1 à R2)

[heroes]

c'est bon, j'ai réussi, merci beaucoup de votre aide :D

Néanmoins, est-ce bien rigoureux d'étudier totue une suite juste sur 2 de ces termes (ici le premier et le second terme) ? Bien que sur cet exercice, je ne vosi pas comment étudier la suite autrement...

[Flodelarab]

c'est bon, j'ai réussi

Réussi à quoi ?
L'énoncé n'a pas de sens.
Et ce que tu nous a écrit est faux. Pour te répondre: NON, on n'étudie pas une suite sur 2 termes.

[heroes]

Mais pour la c), comment trouver la réponse s'il est impossible d'étudier une suite sur seulement 2 termes.
Je sais que ce n'est pas rigoureux, mais je ne vosi pas d'autres solutions...

Si vous pouviez juste répondre à cette question, après je vous laisse tranquil :D

[Flodelarab]

:briques:

Ayéééééééééééé
J'ai retrouvé l'énoncé exact.

Prouver que D(n)=R(n+1)-R(n) est une suite géométrique.
(j'ai inventé D(n) pour des raisons pratiques)

Comment fait-on ? Quelle est la méthode ?
On divise D(n+1) par D(n), et si on trouve une constante alors Dn est une suite géométrique dont la raison est cette constante.


Il te faut donc:
c) exprimer R(n+1) en fonction de Rn et Un. Exprimer U(n+1) en fonction de U(n) et R(n)
d) prouver que D(n) est géométrique (indice: on calcule en fonction de Un et Rn)

à toi :++:

[bombastus]

Bonjour,

Tu te compliques la vie Flodelarab!
L'énoncé a un sens, les suites géométriques ne sont pas Rn et Un mais (Rn-40) et (Un-80), et effectivement, on ne peut pas parler de l'une sans l'autre puisque on a la relation Un+Rn=120.

Donc pour la question c : "Déterminer R(n+1) en fonction de Rn"
commence par exprimer R(n+1) en fonction de Rn et de Un : R(n+1) est obtenu à partir de Rn en soustrayant 10% de la population de Rn et en ajoutant 5% de la population de Un. Quel relation obtiens-tu? (tu peux t'inspirer du calcul de R1 en fonction de R0 et de U0).
Ensuite tu peux remplacer Un par Un=120-Rn et tu obtiens R(n+1) en fonction de Rn.

Pour la d), il faut mettre R(n+1)-40 sous la forme R(n+1)-40 = q(Rn-40) avec q la raison et q=0.85 et c'est gagné.

Puis même raisonnement avec U(n+1)-80 et ce qui est intéressant c'est de regarder ce qui se passe quand n est très grand.

Edit : faute de frappe corrigée...

[Flodelarab]

Tu te compliques la vie Flodelarab!
L'énoncé a un sens, les suites géométriques ne sont pas Rn et Un mais (Rn-80) et (Un-80)

Pitié! Une suite géométrique dont le premier terme est 0 .............
Si tu as trouvé la réponse, n'induit pas le lecteur en erreur stp.


Par contre, Rn=120-Vn, ça c'est utile :++:

[bombastus]

Merci pour l'erreur,

Pitié! Une suite géométrique dont le premier terme est 0 .............
Si tu as trouvé la réponse, n'induit pas le lecteur en erreur stp.

C'est vrai que toi tu as été d'une grande aide pour guider heroes...