Probleme suite associee a une fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Jackychan
- Messages: 6
- Enregistré le: 07 Mar 2013, 14:36
-
 par Jackychan » 07 Mar 2013, 16:30
par Jackychan » 07 Mar 2013, 16:30
Je cale un peu sur un exercice de suite un peu d'aide me serais d'une grande utilité, j'ai ma fonction f(x):x-ln(x²+1) et Uo:1 et Un+1: f(un)
Ici a jai démarrer par :
Initialisation: U0=1 donc U0 [0:1]
Hérédité : supposons que pour un certain n, on ait Un [0:1]
J'ai essayé de faire ca :
Un+1-U0= U0-ln(Un²+1)-1
Un+1-1=1-ln(2)
Un+1=2-ln(2)
Je pense que c'est faux.
Merci d'avance
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 07 Mar 2013, 16:36
par Cheche » 07 Mar 2013, 16:36
f(x) = x - ln(x²+1)
| Uo = 1
| Un+1 = f(Un)
Quelle est ta question ?
-
Jackychan
- Messages: 6
- Enregistré le: 07 Mar 2013, 14:36
-
 par Jackychan » 07 Mar 2013, 18:39
par Jackychan » 07 Mar 2013, 18:39
Pardon, je dois démontrez par réccurence que pour entier n de N Un appartient a [0:1]
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 07 Mar 2013, 19:54
par Cheche » 07 Mar 2013, 19:54
Je n'ai pas trop d'idée
-
Jackychan
- Messages: 6
- Enregistré le: 07 Mar 2013, 14:36
-
 par Jackychan » 07 Mar 2013, 20:11
par Jackychan » 07 Mar 2013, 20:11
D'accord pas grave j' vais attendre d'autre réponses
-
raph107
- Membre Relatif
- Messages: 205
- Enregistré le: 17 Sep 2005, 08:53
-
 par raph107 » 07 Mar 2013, 21:03
par raph107 » 07 Mar 2013, 21:03
Jackychan a écrit:Pardon, je dois démontrez par réccurence que pour entier n de N Un appartient a [0:1]
oui
un appartient à [0;1] donc on a:
0<= un <= 1 ce qui implique que 0<= un² <= 1 et 1<= un² + 1 <= 2 et comme la fonction ln est croissante, on en déduit:
ln(1) <= ln(un² + 1) <= ln(2).
Je te laisse continuer et conclure
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 07 Mar 2013, 21:32
par Cheche » 07 Mar 2013, 21:32
@raph107 Oui, mais tu as un "-" donc je pense que ça ne va pas fonctionner.
Je pense qu'il va falloir dériver la fonction et regarder les variations et en déduire
des bons résultats.
-
raph107
- Membre Relatif
- Messages: 205
- Enregistré le: 17 Sep 2005, 08:53
-
 par raph107 » 07 Mar 2013, 21:36
par raph107 » 07 Mar 2013, 21:36
Cheche a écrit:@raph107 Oui, mais tu as un "-" donc je pense que ça ne va pas fonctionner.
Je pense qu'il va falloir dériver la fonction et regarder les variations et en déduire
des bons résultats.
où est le "-"?
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 07 Mar 2013, 22:39
par Cheche » 07 Mar 2013, 22:39
f(x) = x - ln(x²+1)
Donc tu vas avoir :
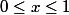
 \leq - ln(x^2+1) \leq 0)
et quand tu fais la somme, tu n'es pas dans [0;1].
-
raph107
- Membre Relatif
- Messages: 205
- Enregistré le: 17 Sep 2005, 08:53
-
 par raph107 » 07 Mar 2013, 22:46
par raph107 » 07 Mar 2013, 22:46
Cheche a écrit:f(x) = x - ln(x²+1)
Donc tu vas avoir :
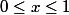
 \leq - ln(x^2+1) \leq 0)
et quand tu fais la somme, tu n'es pas dans [0;1].
f(x) = ln(x²+1) et non pas x- ln(x²+1). Le "-" correspond à une flèche (-->) et non pas au signe -
-
Jackychan
- Messages: 6
- Enregistré le: 07 Mar 2013, 14:36
-
 par Jackychan » 08 Mar 2013, 11:06
par Jackychan » 08 Mar 2013, 11:06
Désolé raph mais c'est bien un moins après le x la fonction est bien x-ln(x²+1), si sa peut vous aider sur l'intervalle [0:1] la fonction est du signe de 1 .
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 08 Mar 2013, 11:31
par Cheche » 08 Mar 2013, 11:31
Jackychan a écrit:Désolé raph mais c'est bien un moins après le x la fonction est bien x-ln(x²+1), si sa peut vous aider sur l'intervalle [0:1] la fonction est du signe de 1 .
Testons la dévirée :
 = \quad x - ln(x^2+1))
 = \quad 1 - \frac{2x}{x^2 +1} \quad = \quad \frac{x^2-2x+1}{x^2 +1})
Après factorisation :
 = \quad \frac{(x-1)^2}{x^2 +1} \geq 0)
Donc f est croissante sur [0;1].
Ainsi cela nous permet de dire que :
Pour tout
 \leq f(x) \leq f(1))
Pour tout
 \leq (1 - ln(2) ) \leq 1)
CQFD
-
Jackychan
- Messages: 6
- Enregistré le: 07 Mar 2013, 14:36
-
 par Jackychan » 08 Mar 2013, 12:10
par Jackychan » 08 Mar 2013, 12:10
Merci Cheche pour ta réponse, mais ce qui me gène ce que je doit rédigée une récurrence pour montrer que Un appartient a [0:1]
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 08 Mar 2013, 12:55
par Cheche » 08 Mar 2013, 12:55
Tu fais ta récurrence sur n.
 \in [0;1] \quad \Longrightarrow \quad<br />U_{n+1} \in [0;1])
CQFD.
-
Jackychan
- Messages: 6
- Enregistré le: 07 Mar 2013, 14:36
-
 par Jackychan » 08 Mar 2013, 13:24
par Jackychan » 08 Mar 2013, 13:24
Merci Cheche ta assurée, une derniere chose je dois déterminer la limite de la suite (Un) cela signifie que je doit déterminée la limite de la fonction ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
