Probleme premiere s maths

[titijuju97]

Bonjour, j'ai complété tout le devoir sauf cet exercice, quelqu'un peu m'aider? merci d'avance :)

Une puce se déplace dans le plan muni d’un repère orthonormé (O ; i , j ) de la façon suivante.
à l’instant t = 0 s, la puce est en O ;
la puce se déplace chaque seconde de façon aléatoire soit de 1 carreau vers la droite et un carreau vers le haut, soit de 1 carreau vers la gauche et de 1 carreau vers le haut ;
la puce s’arrête lorsqu’elle est revenue sur l’axe des ordonnées. Exemples de voyages de la puce
;)

Partie A Simulation

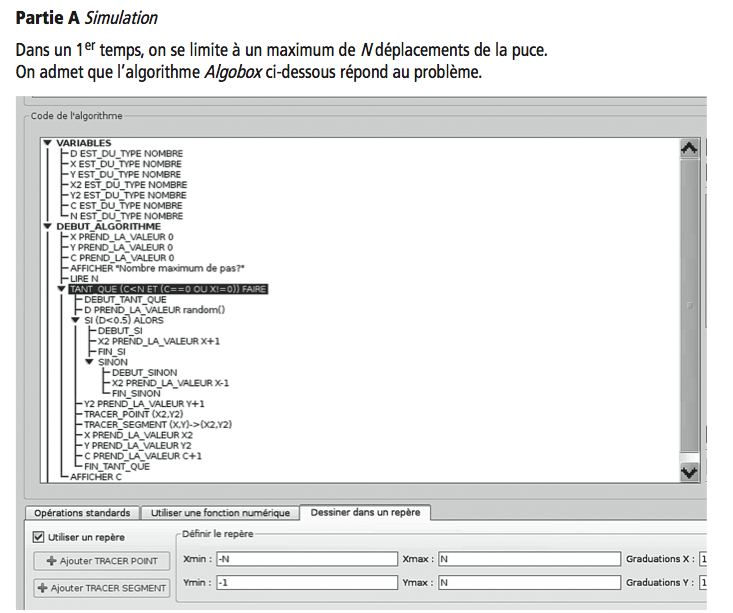
Dans un 1er temps, on se limite à un maximum de N déplacements de la puce.
On admet que l’algorithme Algobox ci-dessous répond au problème.
;) Expliquer la condition C;) Comment simule-t-on un des déplacements aléatoires de la puce ? Expliquer.=
;) Programmer cet algorithme, l’instrumenter.
;) On suppose que N = 8. A partir de cet algorithme, construire un autre algorithme, permettant de simuler 1000 voyages de la puce et de calculer la moyenne des nombres de déplacements de ces différents voyages (pour ce nouvel algorithme, on ne cherchera pas à représenter les différents voyages).
;) Proposer une valeur pour le nombre moyen de déplacements du voyage de la puce. Partie B Modélisation
On suppose toujours que le nombre de déplacements est limité à 8. Chaque voyage de la puce peut être décrit par une liste de –1 et de 1 de longueur au plus N : un –1 correspondant à un déplacement à gauche et 1 à un déplacement à droite.
Par exemple, le voyage 1 peut être décrit par (–1 ; 1) et le voyage 2 par (–1 ; –1 ; –1 ; 1 ; 1 ; –1 ; 1 ; 1). De plus, si la puce a réussi à regagner l’axe des ordonnées, la somme de tous les termes de la suite est nulle.

On note D la variable aléatoire donnant le nombre de déplacements du voyage.

;) Montrer que D peut prendre les valeurs 2, 4, 6 et 8.
;) Déterminer P (D = 2) puis P (D = 4) (on pourra s’aider d’un arbre).
;) Montrer que P (D = 6)= 1 . En déduire P (D = 8). 16
;) Déterminer E(D). Comparer avec les résultats de la partie I

[titijuju97]

Comment fait on pour joindre un fichié?

[paquito]

Le moins que l'on puisse dire est que l'énoncé est peu clair; l'algorithme est incompréhensible; est ce qu'on rentre une valeur de N; que signifie C,X;
sinon simuler un voyage de la puce est facile avec la fonction random();
la condition C
Dans la partie B, P(D=6)=1, signifie que que l'on a toujours D=6. Je vais te donner un programme sur TI pour N=8

:0->X
:0->D
:While X dif o et D<8 ou D=0
:Int(Rand+0,5)->A
:If A=0
:then
:X-1->X
:Else
:X+1->x
:End
:D+1->D
:End
: End
:Disp D

si tu veux D=N tu rajoute Lire N au début et tu remplace 8 par N

Pour simuler 1000 voyages Tu initialise une variable S par 0 au début; Puis tu fait une boucle (For K,1,1000); Tu remplaces Disp D par D+S->S; un end pour le fin pour puis tu affiches S/1000

Je l'ai fait tourner et ça m'a donné une moyenne de 4,26 déplacements;théoriquement ce résultat doit être proche de l'espérance mathématique. sinon, la condition C=0 sert à faire démarrer le programme.

Je ne me suis pas servi d'algobox car je trouve plus facile d'utiliser ma calculatrice; ça donne de toute façon un algorithme écrit en pseudo basic de plus mes programmes sur algobox ne veulent pas souvent marcher!

Sinon, il est évident que les valeurs de D soient 2, 4, 6 ou 8.
L'arbre est assez pénible à réaliser mais faisable jusqu'à 6 déplacements; chaque branche à pour probabilité 1/2; 2 chemins conduisent à D=2, donc p(D=2)=2*1/4=1/2; ensuite sauf erreur de ma part, P(D=4)=1/8, P(D=6)=1/16 et par conséquent P(D=8)=1-1/2-1/8-1/16=5/16.

Je trouve E(D)=4,375, ce qui est en accord avec le 4,26 trouvé sur 1000 simulations (une 2° simulation donne me donne 4,372)

Cet exercice, même si je t'ai beaucoup aidé, va te demander pas mal de travail!




)

[chan79]

Pour compléter, tu peux regarder :ça(on tombe sur une moyenne aux alentours de 4.3)

[titijuju97]

Merci de votre aide! Je ne suis pas sure de comment on attche un fichier... J'essairais l'exercice demain, il est tard chez moi

[titijuju97]

Merci beaucoup de votre aide! J'ai compris la plus part du devoir grace à vous! J'ai encore 3 questions ou je n'ai pas très bien compris.

Pour partie B, la première question, "Montrer que D peut prendre les valeurs 2, 4, 6 et 8." Je ne suis pas sure comment prouver.

Pour partie B la troisième question, je ne sais pas comment prouver que P(D=6) = 1/16

Et pour finir, quelqu'un peut m'explique ce qu'est E(D)? et comment le trouver?

merci beaucoup d'avoir pris le temps de m'expliquer!

[chan79]

Pour partie B, la première question, "Montrer que D peut prendre les valeurs 2, 4, 6 et 8." Je ne suis pas sure comment prouver.

Si la puce fait un certain nombre de déplacements d'un côté, elle devra en faire autant dans l'autre sens pour revenir sur l'axe des y. Donc le nombre de déplacements est pair. (soit 2, 4, 6 ou 8)
Evidemment, au bout des 8 déplacements, elle n'est pas forcément de retour sur l'axe des y.

[titijuju97]

Merci beaucoup!!

"Pour partie B la troisième question, je ne sais pas comment prouver que P(D=6) = 1/16"

"Et pour finir, quelqu'un peut m'explique ce qu'est E(D)? et comment le trouver? "

[paquito]

Il faut faire l'arbre jusqu'à 6 déplacements. Tu verras alors qu'il y a 4 chemins qui conduisent à X=o, donc P(D=6)=4x(1/2)^6=2^2/2^6=1/16.

Si une variable aléatoire finie X prend les valeurs xi avec la probabilité pi=P(X=xi), son espérance mathématiques est E(X)=Sigma des pi.xi; c'est une moyenne théorique.

Ici, E(D)=2xP(D=2)+4xP(D=4)+6xP(D=6)+8xP(D=8).

[titijuju97]

Merci beaucoup!! :)

[chan79]

Les 4 chemins pour une longueur de 6.
Il faut utiliser trois fois le 1 et trois fois le -1. La longueur ne doit être ni 2, ni 4.

[paquito]

Les 4 chemins pour une longueur de 6.
Il faut utiliser trois fois le 1 et trois fois le -1. La longueur ne doit être ni 2, ni 4.

il est clair que des branches s'éliminent au fur et à mesure de la construction de l'arbre; mais on ne peut pas tout détailler!