Problème pour une factorisation

par **Dava31** » 23 Juil 2014, 04:54

Bonjour,

On me demande de factoriser le polynôme suivant :
x^4-5x^2 +4
(lire : x puissance 4 moins 5x puissance 2 +4)

En regardant la réponse à la fin du livre, on doit arriver à :
(x+2)(x-2)(x+1)(x-1)

Je dois avouer que je sèche complétement :) Quelqu'un sait faire? Et peut me faire le détail du calcul pour arriver à cette factorisation?

Merci par avance!

par **chan79** » 23 Juil 2014, 06:28

Dava31 a écrit:Bonjour,

On me demande de factoriser le polynôme suivant :
x^4-5x^2 +4
(lire : x puissance 4 moins 5x puissance 2 +4)

En regardant la réponse à la fin du livre, on doit arriver à :
(x+2)(x-2)(x+1)(x-1)

Je dois avouer que je sèche complétement Quelqu'un sait faire? Et peut me faire le détail du calcul pour arriver à cette factorisation?

Merci par avance!

salut
Pose X=x²

par **Shew** » 23 Juil 2014, 07:11

Dava31 a écrit:Bonjour,

On me demande de factoriser le polynôme suivant :
x^4-5x^2 +4
(lire : x puissance 4 moins 5x puissance 2 +4)

En regardant la réponse à la fin du livre, on doit arriver à :
(x+2)(x-2)(x+1)(x-1)

Je dois avouer que je sèche complétement Quelqu'un sait faire? Et peut me faire le détail du calcul pour arriver à cette factorisation?

Merci par avance!

Bonjour

Ce n'est pas différent que de factoriser un trinome du second degrés . Faites dans un premier temps abstraction du degré et factorisez comme vous le faites d'habitude .

par **WillyCagnes** » 23 Juil 2014, 10:23

bjr
on pose
x^4-5x^2 +4 =0

on peut trouver les racines evidentes comme +1 (la somme des coef +1 -5 +4 =0)
donc on a déjà (x-1) en facteur

puis les autres, il suffit de prendre des nombres entiers de -2 -1 + +1 +2...
donc (x+2)(x+1)(x-2) pour les autres facteurs

au total
(x-1)(x+1)(x-2)(x+2)

par **t.itou29** » 23 Juil 2014, 10:55

On peut aussi écrire :
x^4-5x^2+4=x^2(x^2-4)-(x^2-4)=(x^2-1)(x^2-4)=(x-1)(x+1)(x-2)(x+2)

par **paquito** » 23 Juil 2014, 10:57

Tu écris

et c'est fini (la forme canonique peut toujours servir!).

par **Dava31** » 23 Juil 2014, 16:35

Merci pour vos réponses! Cependant à notre niveau aucune des méthodes que vous proposez n'a été abordé... (x²=X, etc ... on a pas encore vue).

@paquito, tu sembles le faire par complétion de carré, celui ci on l'a vu, seulement...comment es-tu arrivé à une puissance carré? car si tu mets x² en facteur il faut aussi le faire pour la constante 4 et là on se retrouverai avec un 4/x².

@t.itou29, et où est passé le 5 du 5x²?

par **t.itou29** » 23 Juil 2014, 17:33

Dava31 a écrit:Merci pour vos réponses! Cependant à notre niveau aucune des méthodes que vous proposez n'a été abordé... (x²=X, etc ... on a pas encore vue).

@paquito, tu sembles le faire par complétion de carré, celui ci on l'a vu, seulement...comment es-tu arrivé à une puissance carré? car si tu mets x² en facteur il faut aussi le faire pour la constante 4 et là on se retrouverai avec un 4/x².

@t.itou29, et où est passé le 5 du 5x²?

Si tu développes: x^2(x^2-4)-(x^2-4)=x^4-4x^2-x^2+4=x^4-5x^2+4.

par **zygomatique** » 23 Juil 2014, 17:50

salut

quand on ne sait rien ... il suffit de savoir que 5 = 4 + 1 ainsi que les savoirs de collège .... et t.itou29 a donné la réponse la plus élémentaire dans son premier post ....

par **Sake** » 23 Juil 2014, 18:17

zygomatique a écrit:salut

quand on ne sait rien ... il suffit de savoir que 5 = 4 + 1 ainsi que les savoirs de collège .... et t.itou29 a donné la réponse la plus élémentaire dans son premier post ....

Pas la plus élémentaire, mais la plus élégante. La façon standard à ce niveau et de poser X=x^2 comme l'a recommandé Chan.

Une autre façon c'est la forme canonique (classique) :

x^4 - 5x² + 4
= (x² - 5/2)² + (16 - 25)/4
= (x² - 5/2)² - 9/4 = (x² - 5/2 - 3/2)(x² - 5/2 + 3/2) = (x² - 8/2)(x² - 1) = (x - 2)(x + 2)(x - 1)(x + 1)

PS : Ce qu'a fait Paquito, pardon pas vu !

par **zygomatique** » 23 Juil 2014, 18:54

Sake a écrit:Pas la plus élémentaire, mais la plus élégante. La façon standard à ce niveau et de poser X=x^2 comme l'a recommandé Chan.

Une autre façon c'est la forme canonique (classique) :

x^4 - 5x² + 4
= (x² - 5/2)² + (16 - 25)/4
= (x² - 5/2)² - 9/4 = (x² - 5/2 - 3/2)(x² - 5/2 + 3/2) = (x² - 8/2)(x² - 1) = (x - 2)(x + 2)(x - 1)(x + 1)

PS : Ce qu'a fait Paquito, pardon pas vu !

la façon standard est la façon dont travaillent les machines :: elles ne pensent pas elles exécutent des recettes, l'homme lui peut penser ce qu'il lit et créer des idées !!! et remarquer que 5 = 4 + 1

la machine ne détectera jamais que 5 = 4 + 1 donne la réponse (bien qu'elle sache que 5 = 4 + 1 et qu'elle sait compter mieux que moi, même)

:lol3:

une équation bicarrée n'est qu'une simple équation du second degré ... maintenant il suffit de reconnaître la variable .... (c'est la même chose avec un changement de variable dans une intégrale :: c'est simplement une dérivée générique en la variable ...)

:zen:

par **Sake** » 23 Juil 2014, 20:06

zygomatique a écrit:la façon standard est la façon dont travaillent les machines :: elles ne pensent pas elles exécutent des recettes, l'homme lui peut penser ce qu'il lit et créer des idées !!! et remarquer que 5 = 4 + 1

la machine ne détectera jamais que 5 = 4 + 1 donne la réponse (bien qu'elle sache que 5 = 4 + 1 et qu'elle sait compter mieux que moi, même)

:lol3:

une équation bicarrée n'est qu'une simple équation du second degré ... maintenant il suffit de reconnaître la variable .... (c'est la même chose avec un changement de variable dans une intégrale :: c'est simplement une dérivée générique en la variable ...)

:zen:

Par façon standard j'entends façon dont on s'attend à ce qu'il traite l'exo, selon son niveau (typiquement la 1ère S, ici).

Tu le sais bien, tu es prof.

par **Mikihisa** » 23 Juil 2014, 20:25

Pensez a la forme canonique dans ces cas la :

par **Sake** » 23 Juil 2014, 20:27

Pété et répété ;)

par **zygomatique** » 23 Juil 2014, 22:31

Sake a écrit:Par façon standard j'entends façon dont on s'attend à ce qu'il traite l'exo, selon son niveau (typiquement la 1ère S, ici).

Tu le sais bien, tu es prof.

et justement je me bats contre ça ...

en tant que prof je ne veux pas formater un esprit, je veux le former ... donc le laisser libre d'agir et non pas lui imposer des recettes ...

je ne m'attends donc jamais à telle ou telle type de réponse, j'attends seulement une réponse et je me fous du trajet utilisé par mon élève ....

... mais je t'avoue que parfois je baisse les bras ... et j'abandonne cette "utopie" ....( que j'ai vécue en tant qu'élève) ....

par **paquito** » 24 Juil 2014, 10:37

Normalement, la forme canonique a été travaillé en 1°S et elle est efficace, et plus naturelle que de "voir" une astuce permettant une factorisation/

exemple:

, attend de l'élève qu'in applique

,ce qui va aboutir; par contre, on ne s'attend pas a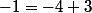

, astuce qui demande de la bouteille et qui ne donne aucun résultat pour

,

on peut toujours essayer une grosse astuce, ça ne marchera pas; donc, une "méthode" qui nécessite un gros coup de bol, ça peut être signalé quand ça se présente (c'est pas inintéressant); mais c'est tout.
Un exemple encore plus simple: factoriser

.

par **chan79** » 24 Juil 2014, 10:58

Autre chemin:

et c'est simple de factoriser cette différence de carrés

Problème pour une factorisation

Problème pour une factorisation

Qui est en ligne