Problème pour conclure dans la justification d'une suite géométrique...

[Anonyme]

Bonjour,

Alors j'ai un exercice qui me demande de calculer les premiers termes de la suite (Un) et de dire si elle est géométrique ou non.

a) Un= (7^n)/5^(n+1)

Voici ce que j'ai fait :

Les premiers termes de cette suite sont :

U_1 = 7/5^2 = 0,28 (environ)
U_2 = 7^2/53 = 0,392 (environ)
U_3 = 7^3/5^4 = 0,5488 (environ)

Ensuite :
U_2/U_1 = 0,392/0,28 = 1,4
U_3/U_2 = 0,5488/0,392 = 1,4

Par conjecture, (U_n) est une suite géométrique de premier terme U_1 = 0,28 et de raison 1,4.

C'est pour la conclusion que je bloque... Je vous montre ce que j'ai fait, dites moi si c'est juste s'il vous plait.

U_n+1/ U_n = ((7^(n+1)/5^((n+1)+1))/(7^n/5^(n+1)
=7^(n+1)/5^((n+1)+1) * 5^(n+1)/ 7n

Et je n'arrive pas à continuer, sans doute parce que c'est faux...

J'espère que c'est lisible, je n'arrive pas à écrire en LaTeX avec mon téléphone...

Aidez-moi à m'en sortir s'il vous plait, pour que je puisse conclure...

Merci d'avance !

[nodjim]

Attends
Un=(7/5)^n * (1/5)
c'est pas une suite géométrique ça ?

[Anonyme]

En fait je crois que j'ai réussi ...

Je fais donc :

U_n+1/ U_n = ((7^(n+1)/5^((n+1)+1))/(7^n/5^(n+1)
= 7^((n+1)-(n+1)+1)/ 7^(n-n+1). (Je calcule les puissances)
=(7/5)/(7/5)
Mais j'ai un problème...
7/5 donne bien 1,4. Mais là j'ai (7/5)/(7/5) et ca me donne 1.

Au final je suis encore bloquée en fait --'

[tototo]

Bonjour,

Un+1/Un= (7^(n+1))/5^(n+2)/ (7^n)/5^(n+1)=7/5 donc Un est géométrique de raison 7/5

[Anonyme]

Attends
Un=(7/5)^n * (1/5)
c'est pas une suite géométrique ça ?

Mais la suite (U_n) n'est pas égale à ça.
(Raaah pourquoi je n'arrive pas à utiliser le LaTeX --')
Je vais allumer mon ordi, et réecrire tout ca sous format LaTeX .

[Luc]

Salut,

U_n+1/ U_n = ((7^(n+1)/5^((n+1)+1))/(7^n/5^(n+1)
=7^(n+1)/5^((n+1)+1) * 5^(n+1)/ (7^n)

Et je n'arrive pas à continuer, sans doute parce que c'est faux...

Non ce n'est pas faux, mais tu peux simplifier un paquet de choses :
et .
Du coup

Remarque que tu n'étais pas obligée de faire ce calcul pénible, il suffisait de remarquer que

[Anonyme]

Bonjour,

Un+1/Un= (7^(n+1))/5^(n+2)/ (7^n)/5^(n+1)=7/5 donc Un est géométrique de raison 7/5

Aah je vois mon erreur... maintenant je peux conclure, merci beaucoup !

[Anonyme]

Salut,


Non ce n'est pas faux, mais tu peux simplifier un paquet de choses :
et .
Du coup

Remarque que tu n'étais pas obligée de faire ce calcul pénible, il suffisait de remarquer que

Ah d'accord merci pour votre réponse !

En fait, c'est le professeur qui veut qu'on suive les étapes comme il nous l'a expliqué.
(déterminer les premiers termes, conjecturer, calculer pour U_n+1/U_n puis conclure... )
Cet exercice je l'avais fait en cours, mais je n'avais pas conclus. je m'étais arrêtée à la conjecture, et conclus en fait par la conjecture ^^
Et donc le professeur m'a fait remarquer qu'il fallait absolument que je conclus avec ce calcul U_n+1/U_n ...

[nodjim]

Ah ces profs .....

[Luc]

La définition d'une suite géométrique, c'est qu'il existe un réel q tel que . Ce n'est pas constante, même si cette propriété est élémentaire et est équivalente à la définition. (En fait, elle ne l'est pas tout à fait car elle n'est pas définie si ).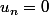

Ça a l'air d'un détail mais c'est important : il est souvent préférable de comprendre les suites "intrinsèquement" grâce à leur forme que de faire des manipulations algébriques hasardeuses, même si ces dernières conduisent presque toujours au résultat.

Par exemple, pour montrer qu'une suite est croissante, un réflexe du lycée est d'étudier le signe de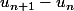 . Sauf que si est définie à l'aide d'une fonction croissante de n, il est plus direct d'invoquer la croissance de cette fonction, et si a une forme multiplicative, il est plus direct de comparer 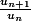à 1, etc.

[Anonyme]

La définition d'une suite géométrique, c'est qu'il existe un réel q tel que . Ce n'est pas constante, même si cette propriété est élémentaire et est équivalente à la définition. (En fait, elle ne l'est pas tout à fait car elle n'est pas définie si ).

Ça a l'air d'un détail mais c'est important : il est souvent préférable de comprendre les suites "intrinsèquement" grâce à leur forme que de faire des manipulations algébriques hasardeuses, même si ces dernières conduisent presque toujours au résultat.

Par exemple, pour montrer qu'une suite est croissante, un réflexe du lycée est d'étudier le signe de . Sauf que si est définie à l'aide d'une fonction croissante de n, il est plus direct d'invoquer la croissance de cette fonction, et si a une forme multiplicative, il est plus direct de comparer à 1, etc.

Hmm d'accord..

Il nous a expliqué qu'il fallait absolument conclure par ce calcul puisque lorsqu'on calcul les premiers termes, il se peut qu'on trouve de bons résultats qui nous montre que cette suite est géométrique. Mais il dit que nous ne pouvons pas dire qu'elle est géométrique vu qu'on n'a pas cherché TOUS les termes. Donc qu'on conjecture.
Et qu'ensuite on fait avec U_n+1/U_n pour pouvoir conclure avec certitude qu'il s'agit vraiment d'une suite géométrique...

[Luc]

Hmm d'accord..

Il nous a expliqué qu'il fallait absolument conclure par ce calcul puisque lorsqu'on calcul les premiers termes, il se peut qu'on trouve de bons résultats qui nous montre que cette suite est géométrique. Mais il dit que nous ne pouvons pas dire qu'elle est géométrique vu qu'on n'a pas cherché TOUS les termes. Donc qu'on conjecture.
Et qu'ensuite on fait avec U_n+1/U_n pour pouvoir conclure avec certitude qu'il s'agit vraiment d'une suite géométrique...

Oui c'est vrai qu'il ne suffit pas d'avoir concordance avec une suite géométrique sur un nombre fini de termes pour assurer que la suite est géométrique. Il faut le démontrer pour TOUS les n.

[Anonyme]

J'ai un autre cas maintenant ...

U_n = 3^n + 3^(n+1)

Je calcule les premiers termes :

U_1 = 3+3^2 = 12
U_2 = 3^2+3^3 = 36
U_3 = 3^3+3^4 = 108

U_2/U_1= 36/12 = 3
U_3/U_2 = 108/36 = 3

Par conjecture, (U_n) est une suite géométrique de premier terme U_1 = 12 et de raison 3


U_(n+1)/U_n = (3^(n+1)+3^(n+1)+1)/(3^(n)+3^(n+1) = (on simplifie avec les puissances qui s'annulent et on trouve :) 3/1 = 3

Donc par conclusion, (U_n) est une suite géométrique de premier terme U_1 = 12 et de raison 3.

Est-ce bon avec cette suite ?


(Le prof' nous a expliqué aussi que si au DS on n'appliquait pas comme il nous l'a appris, on n'aura pas tous les points... DOnc mieux baut que j'applique ce qu'il dit)

[Anonyme]

Oui c'est vrai qu'il ne suffit pas d'avoir concordance avec une suite géométrique sur un nombre fini de termes pour assurer que la suite est géométrique. Il faut le démontrer pour TOUS les n.

Donc voilà, c'est pour cela qu'il nous fait conclure de cette manière là ...

[Luc]

Donc par conclusion, (U_n) est une suite géométrique de premier terme U_1 = 12 et de raison 3.

Est-ce bon avec cette suite ?


(Le prof' nous a expliqué aussi que si au DS on n'appliquait pas comme il nous l'a appris, on n'aura pas tous les points... DOnc mieux baut que j'applique ce qu'il dit)

C'est bon!
Mais là encore, on peut voir directement en factorisant que .

[Anonyme]

C'est bon!
Mais là encore, on peut voir directement en factorisant que .

D'accord
Je vous remercie Luc !