Problème : le paravent chinois
18 messages
- Page 1 sur 1
Problème : le paravent chinois
Bonjour, voici un exercice qui me pose problème :
Un paravent chinois se compose de 3 panneaux rectangulaires de mêmes dimensions.
Les petits côtés, qui seront en contact avec le sol, mesurent 1 mètre.
Ce paravent découpe sur le sol un trapèze ABCD (on supposera que les angles ABC et DCB ont même mesure), ce polygone est le polygone de "sustentation".
Comment choisir les angles ABC et DCB pour que le polygone de "sustentation" ABCD ait une aire maximale.
Voilà, j'ai déjà cherché des solutions avec plusieurs personnes de ma classe mais sans succès alors toute aide sera le bienvenue.
Un paravent chinois se compose de 3 panneaux rectangulaires de mêmes dimensions.
Les petits côtés, qui seront en contact avec le sol, mesurent 1 mètre.
Ce paravent découpe sur le sol un trapèze ABCD (on supposera que les angles ABC et DCB ont même mesure), ce polygone est le polygone de "sustentation".
Comment choisir les angles ABC et DCB pour que le polygone de "sustentation" ABCD ait une aire maximale.
Voilà, j'ai déjà cherché des solutions avec plusieurs personnes de ma classe mais sans succès alors toute aide sera le bienvenue.
Rowman a écrit:Bonjour, voici un exercice qui me pose problème :
Un paravent chinois se compose de 3 panneaux rectangulaires de mêmes dimensions.
Les petits côtés, qui seront en contact avec le sol, mesurent 1 mètre.
Ce paravent découpe sur le sol un trapèze ABCD (on supposera que les angles ABC et DCB ont même mesure), ce polygone est le polygone de "sustentation".
Comment choisir les angles ABC et DCB pour que le polygone de "sustentation" ABCD ait une aire maximale.
Voilà, j'ai déjà cherché des solutions avec plusieurs personnes de ma classe mais sans succès alors toute aide sera le bienvenue.
Soit H le projeté de B sur AD
L'aire est donc la somme de 2 triangles rectangles identiques et d'un rectangle central.
tout dépend de l'angle ABH qui est ABC a qui on a oté 90°
Aire= AHxBH/2+BHxBC+AHxBH/2
Aire= AHxBH + BHxBC
Aire= BH (AH+BC)
Le tout est de calculer AH et BH.
ok?
Bon voilà, c'est encore moi. J'ai presque terminé l'exercice mais je me trouve devant un petit problème de justification.
J'ai dis que x était l'angle ABH (ou l'autre vu que c'est pareil).
J'ai calculé l'aire du trapèze et je trouve cos(x)*(sin(x)+1)
J'ai posé f(x)=cos(x)*(sin(x)+1) et j'ai calculé la dérivée. Je trouve -sin²(x)-sin(x)+cos²(x) ce qui est égale à -sin²(x)-sin(x)+1-sin²(x)
Ensuite je pose X=sin(x) et je me retrouve avec ceci -2X²-X+1
Les racines de ce polynome sont -1 et 1/2
Mon problème est que je ne sais pas sur quel intervalle étudier la fonction, pour l'instant je trouverais que l'aire du trapèze est maximale pour x=1/2 donc que les angles doivent être de pi/3 (je sais pas si j'ai juste)
Un peu d'aide serait la bienvenue. Merci d'avance.
J'ai dis que x était l'angle ABH (ou l'autre vu que c'est pareil).
J'ai calculé l'aire du trapèze et je trouve cos(x)*(sin(x)+1)
J'ai posé f(x)=cos(x)*(sin(x)+1) et j'ai calculé la dérivée. Je trouve -sin²(x)-sin(x)+cos²(x) ce qui est égale à -sin²(x)-sin(x)+1-sin²(x)
Ensuite je pose X=sin(x) et je me retrouve avec ceci -2X²-X+1
Les racines de ce polynome sont -1 et 1/2
Mon problème est que je ne sais pas sur quel intervalle étudier la fonction, pour l'instant je trouverais que l'aire du trapèze est maximale pour x=1/2 donc que les angles doivent être de pi/3 (je sais pas si j'ai juste)
Un peu d'aide serait la bienvenue. Merci d'avance.
Bonjour,
je propose de reprendre un peu. On sait exprimer l'aire du trapèze en fonction de l'angle .
.
Soit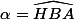 l'angle orienté.
l'angle orienté.
On s'intéresse à l'étude de l'aire du trapèze pour (
(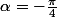 si le paravent est totalement fermé et
si le paravent est totalement fermé et 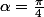 s'il est totalement ouvert). On ne s'intérsse pas au cas
s'il est totalement ouvert). On ne s'intérsse pas au cas  car alors la situation est symétrique.
car alors la situation est symétrique.
On peut donc poser}(sin(\alpha)+1)) .
.
L'aire est maximale si et seulement si f est maximale.
Etude des maxima de f :
Dérivée de f :
Pour tout
=-2sin^2(\alpha)-sin(\alpha)+1) .
.
Soit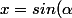) .
.  .
.
Soit .
.
Alors on a\geq0\ \Longleftrightarrow\ g(x)\geq0) .
.
Vous devez maintenant étudier le signe de g en fonction de x, et en déduire le signe de f' en fonction de puis les variations de f en fonction de
puis les variations de f en fonction de  , et enfin les valeurs de
, et enfin les valeurs de  pour lesquelles f est maximale.
pour lesquelles f est maximale.
Bon courage! :we:
je propose de reprendre un peu. On sait exprimer l'aire du trapèze en fonction de l'angle
Soit
On s'intéresse à l'étude de l'aire du trapèze pour
On peut donc poser
L'aire est maximale si et seulement si f est maximale.
Etude des maxima de f :
Dérivée de f :
Pour tout
Soit
Soit
Alors on a
Vous devez maintenant étudier le signe de g en fonction de x, et en déduire le signe de f' en fonction de
Bon courage! :we:
Rowman a écrit:Bon voilà, c'est encore moi. J'ai presque terminé l'exercice mais je me trouve devant un petit problème de justification.
J'ai dis que x était l'angle ABH (ou l'autre vu que c'est pareil).
J'ai calculé l'aire du trapèze et je trouve cos(x)*(sin(x)+1)
J'ai posé f(x)=cos(x)*(sin(x)+1) et j'ai calculé la dérivée. Je trouve -sin²(x)-sin(x)+cos²(x) ce qui est égale à -sin²(x)-sin(x)+1-sin²(x)
Ensuite je pose X=sin(x) et je me retrouve avec ceci -2X²-X+1
Les racines de ce polynome sont -1 et 1/2
Mon problème est que je ne sais pas sur quel intervalle étudier la fonction, pour l'instant je trouverais que l'aire du trapèze est maximale pour x=1/2 donc que les angles doivent être de pi/3 (je sais pas si j'ai juste)
Un peu d'aide serait la bienvenue. Merci d'avance.
Tu te tortures pour rien.
Tu sais que ton angle ABH est compris entre -Pi/2 et Pi/2 (Zébulon, pkoi Pi/4 ?).
ta dérivée est négative si sin(x) est entre 1/2 et 1 et positive si sin(x) entre -1 et 1/2.
Donc ta fonction est croissante sur [-Pi/2;Pi/6] et décroissante sur [Pi/6;Pi/2].
On en déduit un maximum pour ABH de 30°
On en déduit un maximum pour ABC de 120°
L'ouverture est de 120°
je propose de reprendre un peu. On sait exprimer l'aire du trapèze en fonction de l'angle  .
.
Soit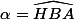 l'angle orienté.
l'angle orienté.
On s'intéresse à l'étude de l'aire du trapèze pour (
(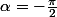 si le paravent est totalement fermé et
si le paravent est totalement fermé et 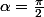 s'il est totalement ouvert). On ne s'intérsse pas au cas
s'il est totalement ouvert). On ne s'intérsse pas au cas  car alors la situation est symétrique.
car alors la situation est symétrique.
On peut donc poser}(sin(\alpha)+1)) .
.
L'aire est maximale si et seulement si f est maximale.
Etude des maxima de f :
Dérivée de f :
Pour tout
=-2sin^2(\alpha)-sin(\alpha)+1) .
.
Soit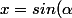) .
.  .
.
Soit .
.
Alors on a\geq0\ \Longleftrightarrow\ g(x)\geq0) .
.
Vous devez maintenant étudier le signe de g en fonction de x, et en déduire le signe de f' en fonction de puis les variations de f en fonction de
puis les variations de f en fonction de  , et enfin les valeurs de
, et enfin les valeurs de  pour lesquelles f est maximale.
pour lesquelles f est maximale.
Soit
On s'intéresse à l'étude de l'aire du trapèze pour
On peut donc poser
L'aire est maximale si et seulement si f est maximale.
Etude des maxima de f :
Dérivée de f :
Pour tout
Soit
Soit
Alors on a
Vous devez maintenant étudier le signe de g en fonction de x, et en déduire le signe de f' en fonction de
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
