Bonjour,
Voici mon problème:
ABCDEFGH est un cube , M est un point mobile de la demi-droite (CG) . on s'intéresse à l'intersection du cube et du tétraèdre MCBD. OU placer le point M pour que le volume de cette intersection soit le tiers du volume du cube ?
Et voici mes recherche:
Volume cube = a^3
Volume tétraèdre = base * hauteur / 3
h=CG+GM=a+y
Volume du grand tétraèdre (T1) :
V(T1)= (a²/2)*(a+y)*(1/3)
=a²/6*(a+y)
=(a^3+a²y)/6
D'après le théorème de Thalès :
On se place dans le triangle MBC. On se place dans le triangle MCD.
Donc MG/MC=MJ/MB=GJ/BC Donc MG/MC=MI/MD=IG/DC
On sait que MG=y On sait que MG=y
MC=(a+y) MC= (a+y)
BC=a DC=a
On a donc : y/(a+y)=GJ/a On a donc : y/(a+y)=IG/a
Alors GJ=ay/(a+y) Alors GI=ay/(a+y)
D'après le théorème de Pythagore :
(AB)² + (AC)² = (BC)²
On se place dans le triangle GIJ.
On sait que GJ=a*y/(a+y)
On sait que GI=a*y/(a+y)
donc (GI)²+(GJ)²=(IJ)²
(IJ)²= (ay/(a+y))² + (ay/(a+y))²
(IJ)²=2a²*y²/(a+y)²
(IJ)=
Volume petit tétraèdre (T2) = base * hauteur / 3
Avec base= (a*y/(a+y))² *1/2
Hauteur= y
donc : V(T2)=(a*y/(a+y))² 1/2 y*1/3
=(a²y^3)/(6(a+y)²)
Volume de la figure dans le cube
V(T0)=V(T1)-V(T2)= a²/6*(a+y)-(a²y^3)/(6(a+y)²)
=(a^3+a²y)/6 –( a²y^3)/(6(a+y)²)
=((a+y)²(a^3+a²y)/(6(a+y)²) – (a²y^3)/(6(a+y)²)
Merci de bien vouloir m'aider à avancer, ce problème est à rendre pour le 28/09/17.
Problème ouvert, Tétraèdre dans un cube
11 messages
- Page 1 sur 1
Problème ouvert, Tétraèdre dans un cube
Modifié en dernier par TS4ENGALERE le 24 Sep 2017, 20:22, modifié 2 fois.
Re: Problème ouvert, Tétraèdre dans un cube
Bonsoir,
Quand vous dîtes "le volume de l'intersection entre le cube et le tétraèdre", vous voulez dire "le volume du cube et du tétraèdre" ?
Si oui,
 , où
, où 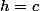 et
et  , avec
, avec  .
.
Nous imposons .
.
Donc , à résoudre pour
, à résoudre pour  . (
. ( peut être en dehors du cube mais appartient à la demi-droite CG).
peut être en dehors du cube mais appartient à la demi-droite CG).
Si non,
Il faut étudier le volume de la nouvelle figure géométrique car il y a une intersection entre BM et FG (il ne s'agit plus d'un tétraèdre).
Quand vous dîtes "le volume de l'intersection entre le cube et le tétraèdre", vous voulez dire "le volume du cube et du tétraèdre" ?
Si oui,
Nous imposons
Donc
Si non,
Il faut étudier le volume de la nouvelle figure géométrique car il y a une intersection entre BM et FG (il ne s'agit plus d'un tétraèdre).
Modifié en dernier par Bigorneau le 24 Sep 2017, 19:19, modifié 1 fois.
Re: Problème ouvert, Tétraèdre dans un cube
Bonsoir,
sur la figure que nous a donné le prof, le point M est hors du cube donc j'ai fais V(cube)/3 = V(grand tétraèdre) - V(petit tétraèdre ( calculé grâce au théorème de Thalès))
sur la figure que nous a donné le prof, le point M est hors du cube donc j'ai fais V(cube)/3 = V(grand tétraèdre) - V(petit tétraèdre ( calculé grâce au théorème de Thalès))
Re: Problème ouvert, Tétraèdre dans un cube
Oui, on peut d'abord regarder si 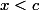 (ce la revient à solutionner le cas simple écrit ci-haut), sauf qu'il n'existe pas de solution.
(ce la revient à solutionner le cas simple écrit ci-haut), sauf qu'il n'existe pas de solution.
Alors , et nous étudions
, et nous étudions 
où .
.
 (volume du grand tétraèdre)
(volume du grand tétraèdre)
\times (x-c)}{6}) (volume du petit tétraèdre,
(volume du petit tétraèdre, 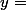 point intersection entre DM et GH ;
point intersection entre DM et GH ;  point d'intersection entre BM et FG)
point d'intersection entre BM et FG)
Il reste à exprimer y et z en fonction de x.
Faites un repère cartésien. L'équation des droites BM et DM peuvent être écrites, puis évaluez au point G pour trouver y et z.
Alors
où
Il reste à exprimer y et z en fonction de x.
Faites un repère cartésien. L'équation des droites BM et DM peuvent être écrites, puis évaluez au point G pour trouver y et z.
Modifié en dernier par Bigorneau le 24 Sep 2017, 19:44, modifié 2 fois.
Re: Problème ouvert, Tétraèdre dans un cube
TS4ENGALERE a écrit:
Volume de la figure dans le cube
V(T0)=V(T1)-V(T2)= a²/6*(a+y)-a²y^3/(6(a+y)²)
=(a^3+a²y)/6 – a²y^3/(6(a+y)²
=((a+y)²(a^3+a²y) – a²y^3)/(6(a+y)²
salut
un 6 a disparu à la dernière ligne
Ton raisonnement est correct
Tu dois trouver y=a*N avec N = nombre d'or=
Re: Problème ouvert, Tétraèdre dans un cube
chan79 a écrit:TS4ENGALERE a écrit:
Volume de la figure dans le cube
V(T0)=V(T1)-V(T2)= a²/6*(a+y)-a²y^3/(6(a+y)²)
=(a^3+a²y)/6 – a²y^3/(6(a+y)²
=((a+y)²(a^3+a²y) – a²y^3)/(6(a+y)²
salut
un 6 a disparu à la dernière ligne
Ton raisonnement est correct
Tu dois trouver y=a*N avec N = nombre d'or=
salut, on a pas encore entendu parler des nombre d'or, je pense aussi trouvé un résultat sous forme Y=a*N avec N mais je ne vois pas comment ^^
V(T0)=V(T1)-V(T2)= a²/6*(a+y)-(a²y^3)/(6(a+y)²)
=(a^3+a²y)/6 –( a²y^3)/(6(a+y)²)
=((a+y)²(a^3+a²y)/(6(a+y)²) – (a²y^3)/(6(a+y)²)
Modifié en dernier par TS4ENGALERE le 24 Sep 2017, 20:23, modifié 3 fois.
Re: Problème ouvert, Tétraèdre dans un cube
Bigorneau a écrit:Oui, on peut d'abord regarder si(ce la revient à solutionner le cas simple écrit ci-haut), sauf qu'il n'existe pas de solution.
Alors, et nous étudions
où.
(volume du grand tétraèdre)
(volume du petit tétraèdre,
point intersection entre DM et GH ;
point d'intersection entre BM et FG)
Il reste à exprimer y et z en fonction de x.
Faites un repère cartésien. L'équation des droites BM et DM peuvent être écrites, puis évaluez au point G pour trouver y et z.
Notre prof nous avais guidé sur le même chemin que Chan79, juste je n'arrive pas a isoler le Y
pour avoir un résultat de forme Y=a*N
Re: Problème ouvert, Tétraèdre dans un cube
tu as écrit
((a+y)²(a^3+a²y)/(6(a+y)²) – (a²y^3)/(6(a+y)²)
cela donne
^3-a^2 y^3}{6(a+y)^2}=\frac{a^2 (a^3+3a^2y+3ay^2+y^3)-a^2 y^3}{6(a+y)^2})
}{6(a+y)^2}})
il faut résoudre
}{6(a+y)^2}}=\frac{a^3}{3})
^2)
je te laisse finir
((a+y)²(a^3+a²y)/(6(a+y)²) – (a²y^3)/(6(a+y)²)
cela donne
il faut résoudre
je te laisse finir
- Fichiers joints
-
- ima1.gif (6.27 Kio) Vu 918 fois
Re: Problème ouvert, Tétraèdre dans un cube
Merci de m'avoir aidé, je ne met pas ma démarche car je sais que certain de mes camarades ne vont pas se gêner pour tout recopier sans faire aucun effort, mais j'en suis arrivé à Y= a ((racine(5)+1)/2).
Encore merci
Encore merci
Modifié en dernier par TS4ENGALERE le 25 Sep 2017, 19:36, modifié 1 fois.
Re: Problème ouvert, Tétraèdre dans un cube
TS4ENGALERE a écrit: mais j'en suis arrivé à Y= a ((racine(5)-1)/2).
Encore merci
Y= a ((racine(5)+1)/2)
Re: Problème ouvert, Tétraèdre dans un cube
chan79 a écrit:TS4ENGALERE a écrit: mais j'en suis arrivé à Y= a ((racine(5)-1)2).
Encore merci
Y= a ((racine(5)+1)/2)
oui je viens de me rendre compte de mon erreur en recopiant. Merci
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
