Un problème ouvert
53 messages
- Page 2 sur 3 - 1, 2, 3
J'ai une autre idée.
En considérant le produit vectoriel de et
et  noté
noté  et en remarquant que
et en remarquant que  et
et  ne sont pas colinéaires,
ne sont pas colinéaires,
on a où
où  .
.
J'ai donc, d'après les formules du sinus
 que je peux aussi écrire
que je peux aussi écrire
 , j'en déduis que
, j'en déduis que
 et là j'ai même plus besoin de conjecturer le fait que le triangle GHI soit rectangle, je peux directement tomber sur le résultat.
et là j'ai même plus besoin de conjecturer le fait que le triangle GHI soit rectangle, je peux directement tomber sur le résultat.
En considérant le produit vectoriel de
 et
et  noté
noté  et en remarquant que
et en remarquant que  et
et  ne sont pas colinéaires,
ne sont pas colinéaires, on a
 où
où  .
.J'ai donc, d'après les formules du sinus
 que je peux aussi écrire
que je peux aussi écrire  , j'en déduis que
, j'en déduis que  et là j'ai même plus besoin de conjecturer le fait que le triangle GHI soit rectangle, je peux directement tomber sur le résultat.
et là j'ai même plus besoin de conjecturer le fait que le triangle GHI soit rectangle, je peux directement tomber sur le résultat.Je m'explique.
Je veux calculer l'aire du triangle en connaissant les coordonnées de ses sommets dans le repère orthonormal que j'ai (grâce au fait que ABC rectangle en A).
Pour ça je vais imaginer le parallélograme GIHJ tel que .
.
Or, je sais que l'aire de ce parallélograme, définit par les vecteurs
de ce parallélograme, définit par les vecteurs  et
et  , est la norme de leur produit vectoriel, tel que
, est la norme de leur produit vectoriel, tel que  .
.
J'en déduis donc que l'aire de mon triangle est égale à la moitié de
de mon triangle est égale à la moitié de  , soit
, soit  . Je peux ensuite, en utilisant les coordonnées des points trouver mon résultat.
. Je peux ensuite, en utilisant les coordonnées des points trouver mon résultat.
Mon raisonnement te parait-il bon ?
Je veux calculer l'aire du triangle en connaissant les coordonnées de ses sommets dans le repère orthonormal que j'ai (grâce au fait que ABC rectangle en A).
Pour ça je vais imaginer le parallélograme GIHJ tel que
 .
.Or, je sais que l'aire
 de ce parallélograme, définit par les vecteurs
de ce parallélograme, définit par les vecteurs  et
et  , est la norme de leur produit vectoriel, tel que
, est la norme de leur produit vectoriel, tel que  .
.J'en déduis donc que l'aire
 de mon triangle est égale à la moitié de
de mon triangle est égale à la moitié de  , soit
, soit  . Je peux ensuite, en utilisant les coordonnées des points trouver mon résultat.
. Je peux ensuite, en utilisant les coordonnées des points trouver mon résultat.Mon raisonnement te parait-il bon ?
Encore une fois, ce n'est pas ton raisonnement en soi qui n'est pas bon mais juste le fait que tu utilises un produit vectoriel là où il ne peut exister !
Comment définis-tu ou même calcules-tu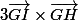 ?
?
Le produit vectoriel ne se définit pas dans R^2, la seule chose que tu peux faire c'est plonger le plan dans l'espace en fixant qu'un point (a,b) du plan est un point (a,b,0) dans l'espace.
Comment définis-tu ou même calcules-tu
Le produit vectoriel ne se définit pas dans R^2, la seule chose que tu peux faire c'est plonger le plan dans l'espace en fixant qu'un point (a,b) du plan est un point (a,b,0) dans l'espace.
Nightmare a écrit: Comment définis-tu ou même calcules-tu?
En fait j'utilise une relation qui me permet justement de ne pas travailler avec cette expression.
Je définis
 avec
avec  , c'est à dire en revenant sur quelque chose que je connais.
, c'est à dire en revenant sur quelque chose que je connais.Nightmare a écrit:Le produit vectoriel ne se définit pas dans R^2, la seule chose que tu peux faire c'est plonger le plan dans l'espace en fixant qu'un point (a,b) du plan est un point (a,b,0) dans l'espace.
J'entends bien oui, mais justement, quand je parle de produit vectoriel dans ce cas-là ce n'est pas en sous-entendant que je le fais dans un espace de dimension 2 (je ne peux pas le faire) mais en ne disant rien. Je pense que tu veux me dire qu'il faut plutôt que je précise qu'on est en dimension 3 et rajouter une cote nulle ? Ok, je comprends bien.
Le produit vectoriel ne vaut pas ce que tu as écrit.
Je pense qu'il vaut mieux que tu oublies cet outil pour le moment.
Le produit vectoriel, contrairement au produit scalaire est un vecteur (il est à valeur vectorielle) alors que le produit scalaire est un nombre (un scalaire).
Ce que tu as écrit (en remplaçant cos par sin et en mettant des valeurs absolues) n'est pas le produit vectoriel de GI et GH mais sa norme !
Je pense qu'il vaut mieux que tu oublies cet outil pour le moment.
Le produit vectoriel, contrairement au produit scalaire est un vecteur (il est à valeur vectorielle) alors que le produit scalaire est un nombre (un scalaire).
Ce que tu as écrit (en remplaçant cos par sin et en mettant des valeurs absolues) n'est pas le produit vectoriel de GI et GH mais sa norme !
bonsoir,
avec les coordonnées barycentriques de I,H,G
on obtient par le théorème de Thalès les coordonnées suivantes
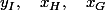
Ces coordonnées sont les mesures de longueurs des hauteurs
de triangles dont il est intéressant de calculer les aires.
Les calculs d'aire avec la formule Base x Hauteur/2 donnent
les aires en proportion de l'aire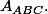
avec les coordonnées barycentriques de I,H,G
on obtient par le théorème de Thalès les coordonnées suivantes
Ces coordonnées sont les mesures de longueurs des hauteurs
de triangles dont il est intéressant de calculer les aires.
Les calculs d'aire avec la formule Base x Hauteur/2 donnent
les aires en proportion de l'aire
Salut tout le monde,
pour ceux que ça intéresse (on ne sait jamais :id:) voici une correction détaillée (qui n'est pas de moi).
On prendra comme référence le schéma suivant.
[url="http://img79.imageshack.us/i/p0610091644.jpg/"] [/url]
[/url]
On notera A(GHI) l'aire du triangle GHI.
Q est le barycentre de (B,2)(C,1) et A, G, D sont alignés donc G est barycentre de (A,a)(D,3), par associativité G est barycentre de (B,2)(A,a)(C,1) avec a réel.
De même, E est barycentre de (A,1)(C,2) et E, I, B sont alignés donc G est barycentre de (B,b)(A,1)(C,2) avec b réel. On a donc G barycentre de (B,b)(A,1)(C,2) et de (B,4)(A,2a)(C,2).
Par identification, b=4 et a=1/2 donc G est barycentre de (B,4)(A,1)(C,2).
De même, on trouve I barycentre de (B,1)(A,2)(C,4) et H barycentre de (B,2)(A,4)(C,1).
Le milieu de [AG] est barycentre de (A,7)(G,7) soir de (A,7)(B,4)(A,1)(C,2) et (en regroupant et en simplifiant par 2) de (B,2)(A,4)(C,1). Par unicité du barycentre, c'est donc H.
De même, G est le milieu de [BE] et I milieu de [HC].
(GH) est médiane du triangle HBI donc A(BHG)=A(GHI), et (BH) est médiane du triangle GBA donc A(GHB)=A(BHA).
On a donc A(GBA)=2A(GHI).
De même A(BCE)=2A(GHI) et A(AHC)=2A(GHI).
On obtient A(ABC)=(2+2+2+1)A(GHI)=7A(GHI).
Soit 7A(GHI) et A(GHI)=150m²
7A(GHI) et A(GHI)=150m²
pour ceux que ça intéresse (on ne sait jamais :id:) voici une correction détaillée (qui n'est pas de moi).
On prendra comme référence le schéma suivant.
[url="http://img79.imageshack.us/i/p0610091644.jpg/"]
 [/url]
[/url]On notera A(GHI) l'aire du triangle GHI.
Q est le barycentre de (B,2)(C,1) et A, G, D sont alignés donc G est barycentre de (A,a)(D,3), par associativité G est barycentre de (B,2)(A,a)(C,1) avec a réel.
De même, E est barycentre de (A,1)(C,2) et E, I, B sont alignés donc G est barycentre de (B,b)(A,1)(C,2) avec b réel. On a donc G barycentre de (B,b)(A,1)(C,2) et de (B,4)(A,2a)(C,2).
Par identification, b=4 et a=1/2 donc G est barycentre de (B,4)(A,1)(C,2).
De même, on trouve I barycentre de (B,1)(A,2)(C,4) et H barycentre de (B,2)(A,4)(C,1).
Le milieu de [AG] est barycentre de (A,7)(G,7) soir de (A,7)(B,4)(A,1)(C,2) et (en regroupant et en simplifiant par 2) de (B,2)(A,4)(C,1). Par unicité du barycentre, c'est donc H.
De même, G est le milieu de [BE] et I milieu de [HC].
(GH) est médiane du triangle HBI donc A(BHG)=A(GHI), et (BH) est médiane du triangle GBA donc A(GHB)=A(BHA).
On a donc A(GBA)=2A(GHI).
De même A(BCE)=2A(GHI) et A(AHC)=2A(GHI).
On obtient A(ABC)=(2+2+2+1)A(GHI)=7A(GHI).
Soit
 7A(GHI) et A(GHI)=150m²
7A(GHI) et A(GHI)=150m²bonsoir,
moi aussi , je me suis fendu d'un énoncé du même style (pro domo)
Tim,
est ce que tu identifes modulo un facteur multiplicatif ? (ça fait une inconnue de plus). Personnellement, je travaille avec une somme de poids égale à 1
comment dit-on ? coordonnées homogènes normalisées ?
ce qui fait que deux coeff du style a+d=1 avec D(d), D \in [B,C])
se répartissent par associativité sur B(b) et C(c) en)
Zweig,
pour obtenir la proportionnalité des aires,passes-tu par des pieds de perpendiculaires et doit distinguer le cas où le triangle ABC a un angle obtu ?
moi aussi , je me suis fendu d'un énoncé du même style (pro domo)
Timothé Lefebvre a écrit:Par identification, b=4 et a=1/2 donc G est barycentre de (B,4)(A,1)(C,2).
Tim,
est ce que tu identifes modulo un facteur multiplicatif ? (ça fait une inconnue de plus). Personnellement, je travaille avec une somme de poids égale à 1
comment dit-on ? coordonnées homogènes normalisées ?
ce qui fait que deux coeff du style a+d=1 avec
se répartissent par associativité sur B(b) et C(c) en
Zweig,
pour obtenir la proportionnalité des aires,passes-tu par des pieds de perpendiculaires et doit distinguer le cas où le triangle ABC a un angle obtu ?
53 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

 [/CENTER]
[/CENTER]