Problème notation somme

[t.itou29]

Bonsoir,
Dans un exercice (sur la fonction de Moebius) j'ai une fonction définie par:



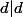
Je comprends que la somme est indexée par les diviseurs d de n mais qu'en est-il pour g(d) ? Ça donne en indice mais quel sens cela a-t-il ?

[Manny06]

Bonsoir,
Dans un exercice (sur la fonction de Moebius) j'ai une fonction définie par:



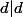
Je comprends que la somme est indexée par les diviseurs d de n mais qu'en est-il pour g(d) ? Ça donne en indice mais quel sens cela a-t-il ?

d est un diviseur quelconque de n (en supposant qu'on ne prend que les diviseurs positifs
par exemple si n est premier
g(n)=f(1)+f(n)

[morpho]

Bonsoir,
Dans un exercice (sur la fonction de Moebius) j'ai une fonction définie par:



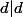
Je comprends que la somme est indexée par les diviseurs d de n mais qu'en est-il pour g(d) ? Ça donne en indice mais quel sens cela a-t-il ?

Explication:
La notation signifie: "on somme sur tous les diviseurs de n" , c'est une simple abréviation de cette phrase, (comme des SMS)

donc quelque soit n , on sait ses diviveurs ==> donc on sait sommer !!!!
si n est premier , la somme comporte 2 ternes, puisqu'il n'y a que 2 diviseurs.
sinon ==> on somme sur tous les diviseurs de n.

[Sylviel]

Autre manière de voir les choses :
dans ton expression tu peux remplacer d par m, delta, ou une petite fleur ! ce sera toujours pareil.

Donc si tu calcules g(d), le d dans "g(d)" n'a rien à voir avec celui de ta somme...

[t.itou29]

Autre manière de voir les choses :
dans ton expression tu peux remplacer d par m, delta, ou une petite fleur ! ce sera toujours pareil.

Donc si tu calcules g(d), le d dans "g(d)" n'a rien à voir avec celui de ta somme...

Oui c'est ça qui me bloquait j'avais compris que la somme était indexée sur les diviseurs de n mais j'avais pas compris que si je fait g(d), le d n'a rien à voir à c celui de la somme.

[t.itou29]

Maintenant que j'ai compris la notation je bloque sur l'exo en lui-même:
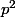
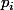
On défint la fonction de Moebius par , si n est divisible par avec p un certain nombre premier et si les sont des premiers deux à deux distincts.
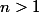
1) Montrer que pour tout , on a:

2) En déduire que si est une fonction et si g est définie par la formule:

Alors on peut retrouver f à partir de la formule:


J'ai réussi la 1) mais je sèche sur la 2). J'ai remarqué que mais après comment l'utiliser...