Problème Maths : fonction trinôme
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
toitoinec2
- Membre Naturel
- Messages: 38
- Enregistré le: 01 Avr 2014, 21:28
-
 par toitoinec2 » 19 Sep 2014, 17:23
par toitoinec2 » 19 Sep 2014, 17:23
mathelot a écrit:on fait une étude de signe de
)
en le factorisant
=-4(l^2 - 3200))
Pk 3200 ? Et après ca on fait quoi ?
-
mathelot
 par mathelot » 19 Sep 2014, 17:24
par mathelot » 19 Sep 2014, 17:24
=-4(l^2 - 3200)=-4(l-40\sqrt{2})(l+40\sqrt{2}))
car
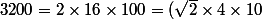^2)
apprendre par coeur le résultat:
le trinome est du signe de "a" à l'extérieur de l'intervalle des racinesici, tu as deux trinomes:
un premier de la variable

avec des coefficients en

dont on calcule le discriminant,
un second de la variable

avec des coefficients constants
-
toitoinec2
- Membre Naturel
- Messages: 38
- Enregistré le: 01 Avr 2014, 21:28
-
 par toitoinec2 » 19 Sep 2014, 17:31
par toitoinec2 » 19 Sep 2014, 17:31
Comment on fait pour faire l'étude du signe avéc ce resultat ?
-
mathelot
 par mathelot » 19 Sep 2014, 17:33
par mathelot » 19 Sep 2014, 17:33
keofran a écrit:
on factorise par -4.le deuxieme terme donne 3200
-
mathelot
 par mathelot » 19 Sep 2014, 17:34
par mathelot » 19 Sep 2014, 17:34
as tu un paragraphe intitulé
"signe du trinome du second degré" dans ton cours ?
une fois factorisé, le trinome s'écrit
(x-x_2))
où
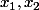
sont ses racines
-
toitoinec2
- Membre Naturel
- Messages: 38
- Enregistré le: 01 Avr 2014, 21:28
-
 par toitoinec2 » 19 Sep 2014, 17:36
par toitoinec2 » 19 Sep 2014, 17:36
Oui mais trouve le signe il faut calculer le discrimant et ensuite trouver les solutions et après faire le tableau !! Mais la comment ont fait vu qu'on a l ?
-
mathelot
 par mathelot » 19 Sep 2014, 17:39
par mathelot » 19 Sep 2014, 17:39
c'est un exo à tiroirs.
Une longueur du côté s'appelle

Elle
existe et est racine d'un trinome en x.
Ce trinome a un discriminant
)
trinome en

On est en train de factoriser
)
pour connaitre les valeurs de

qui le rende positif
-
mathelot
 par mathelot » 19 Sep 2014, 17:43
par mathelot » 19 Sep 2014, 17:43
ça coince où ?
-
toitoinec2
- Membre Naturel
- Messages: 38
- Enregistré le: 01 Avr 2014, 21:28
-
 par toitoinec2 » 19 Sep 2014, 17:52
par toitoinec2 » 19 Sep 2014, 17:52
mathelot a écrit:ça coince où ?
Oui mais comment on fait pour trouver ces valeurs de x après avoir factoriser ?
-
toitoinec2
- Membre Naturel
- Messages: 38
- Enregistré le: 01 Avr 2014, 21:28
-
 par toitoinec2 » 19 Sep 2014, 17:52
par toitoinec2 » 19 Sep 2014, 17:52
toitoinec2 a écrit:Oui mais comment on fait pour trouver ces valeurs de x après avoir factoriser ?
Valeur de l pardon ?
-
mathelot
 par mathelot » 19 Sep 2014, 18:31
par mathelot » 19 Sep 2014, 18:31
En étudiant le signe de
=-4(l-40\sqrt{2})(l+40\sqrt{2}))
selon les valeurs de

à l'aide d'un tableau de signes.

-
toitoinec2
- Membre Naturel
- Messages: 38
- Enregistré le: 01 Avr 2014, 21:28
-
 par toitoinec2 » 19 Sep 2014, 22:22
par toitoinec2 » 19 Sep 2014, 22:22
mathelot a écrit:En étudiant le signe de
=-4(l-40\sqrt{2})(l+40\sqrt{2}))
selon les valeurs de

à l'aide d'un tableau de signes.

Et c'est ca c'est le resultat final ?
-
mathelot
 par mathelot » 20 Sep 2014, 08:05
par mathelot » 20 Sep 2014, 08:05
il s'agit de comprendre (que tu comprennes) le résultat suivant
 \geq 0 \Leftrightarrow l \in [-40\sqrt{2};40\sqrt{2}] \cap [40;+\infty[)
le 1r intervalle pour que le discriminant soit positif, le second à cause de
l'inégalité triangulaire
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 20 Sep 2014, 08:34
par Shew » 20 Sep 2014, 08:34
mathelot a écrit:En étudiant le signe de
=-4(l-40\sqrt{2})(l+40\sqrt{2}))
selon les valeurs de

à l'aide d'un tableau de signes.

N'y a t'il pas une erreur d'orientation de signe dans ce cas la ?
Ne devrait on pas avoir
 \ge 0 \Leftrightarrow -4(l - 40\sqrt{2})(l + 40\sqrt{2}) \ge 0 \Leftrightarrow (l - 40\sqrt{2})(l + 40\sqrt{2}) \le 0)
???
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 225 invités
en le factorisant