Problème Maths : fonction trinôme

[toitoinec2]

Bonjour ,
Voici mon problème auquel je n'y arrive pas :(

2 clous A et B sont distants de 40 cm
On note l la longueur de la ficelle
Déterminer les valeurs de l pour lesquelles il est possible de tendre la ficelle de façon que le triangle ABC soit rectangle en C.

SVP aidez moi car je suis bloqué

[mathelot]

bonjour,

en coordonnées avec


il reste à étudier les variations de cette fonction, pour l'angle au centre
(l'angle que fait la médiane avec l'hypotènuse)

[keofran]

Le triangle ABC est rectangle en C si l'égalité de Pythagore est vérifiée.

En nommant x le côté AC et l-x le côté BC, qu'obtiens-tu comme égalité ?

[keofran]

Pour vérifier on peut faire un schéma. Le point C se situe sur le cercle de diamètre [AB]. On voit immédiatement que l est compris entre 40 et longueur de l quand C est équidistant de A et B sur le cercle (ce qui correspond à de mathelot même si sa méthode me paraît un peu compliquée pour un élève qui débute la première S et qui n'a vu ni dérivation, ni l'étude des fonctions trigo)

D'ailleurs une première condition sur l qui découle de l'inégalité triangulaire :

[toitoinec2]

Je ne comprends rien à votre raisonnement ! Il y a une méthode plus simple pour un élève de 1er S ?

[mathelot]

oui, suis la méthode de kéofran.....et applique Pythagore:

Le triangle ABC est rectangle en C si l'égalité de Pythagore est vérifiée.

En nommant x le côté AC et l-x le côté BC, qu'obtiens-tu comme égalité ?

[toitoinec2]

J'obtiens

AB^2=AC^2+BC^2
40^2=x^2+(l-x)^2
1600=x^2+l^2-2lx+x^2
1600=2x^2+l^2-2lx
2x^2+l^2-2lx-1600

C'est sa ?

[keofran]

Oui avec "=0"

Ce qui donne en clair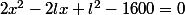

Puisque cette égalité doit être vraie pour que le triangle ABC soit rectangle, il faut donc qu'il existe au moins une solution pour x ...

[toitoinec2]

Comment on fait pour trouver la solution ? Avéc le discrimant ? Mais c'est pas une fonction trinôme ?

[keofran]

Si l'on prend x pour l'inconnue, on a bien la forme ax²+bx+c=0

[toitoinec2]

C'est à dire ? Du coup c'est quoi le calcul ?

[toitoinec2]

Ca donne l^2+2lx-1600 ?

[keofran]

Je ne comprends pas ce que tu fais.

On a une équation en x du type ax²+bx+c = 0 avec :
a=2
b=-2l
c=l²-1600

Pas grave si l n'est pas connu, ça reste un nombre !

Pour que cette équation ait au moins une solution réelle il faut que le discriminant soit positif ou nul.
Que vaut ce discriminant ?

[toitoinec2]

Le discrimant est égal a 4l^2-8+2l^2-1600 c'est sa ?

[keofran]

Non, le discriminant est égal à b²-4ac.

En remplaçant ça donne (-2l)²-4*2*(l²-1600)

Développe et simplifie.

[toitoinec2]

Je trouve un discrimant négatif :( j'obtiens en développant : 4l^2-8-8l^2+12800
-4l^2+12792 c'est sa ?

[keofran]

C'est presque ça mais je ne comprends pas d'où vient le -8 et je ne comprends pas pourquoi tu considères que le discriminant est négatif.

Le développement se fait ainsi :


A quelle condition sur le discriminant l'équation possède au moins une solution en x ?

Ce qui donnera une seconde condition sur l et ainsi un encadrement pour l.

[toitoinec2]

Mais comment on fait pour trouver les solutions avec un l ?
Et comment on trouve l'encadrement ?

[mathelot]

on fait une étude de signe de en le factorisant

[toitoinec2]

Donc ça donne quoi ?