Probleme de maths 2nd (réflexion)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
axel031
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Nov 2009, 11:49
-
 par axel031 » 01 Nov 2009, 11:56
par axel031 » 01 Nov 2009, 11:56
Bonjour, je viens de m'inscrire en fait et j'aimerais que vous m'aidiez pour un problème de maths ... je me casse la tête depuis pas mal de temps déjà et je n'ai toujours pas de résultat valable, je vous le remet intégralement :
Soient a et b deux réels tels que 0 ;) a ;) b .
Factoriser les expressions ;)ab - a et b - ;)ab. (résolu)
En déduire que ;)ab est compris entre a et b, (résolu)
et qu'il est plus proche de a que de b. (Problème aie aie)
Voila, la dernière question me pause vraiment un problème, je n ai pas véritablement de démonstration qui le prouve ... Auriez vous une idée s'il vous plait ? Merci :we:
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 01 Nov 2009, 12:00
par Timothé Lefebvre » 01 Nov 2009, 12:00
Salut,
compare les racines de a et b, puis multiplie par le facteurs de tes factorisations : qu'obtiens-tu ?
Ensuite tu fais un petit remplacement judicieux pour obtenir la comparaison entre différence entre la racine de ab et les entiers a et b.
-
axel031
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Nov 2009, 11:49
-
 par axel031 » 01 Nov 2009, 12:10
par axel031 » 01 Nov 2009, 12:10
Excuse moi mais je suis nouveau alorrrs je te suis pas tres bien ...
si je te suis j'ai : ;)a - ;)b = ;)a(;)b -;)a) - ;)b(;)b-;)a)
= ;)ab - a - (b - ;)ab)
= ;)ab -a -b + ;)ab
= 2;)ab - a - b ...
Je te suis pas très bien la ... je vais peut être trop loin dans mes calculs ... ?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 01 Nov 2009, 12:15
par Timothé Lefebvre » 01 Nov 2009, 12:15
Qu'as-tu trouvé comme factorisations ?
Regarde bien, on a :
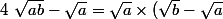)
Et comme

Or
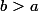
, on a :

Quel est le signe de leur produit ?
Qu'en déduire ?
Je te laisse continuer.
-
axel031
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Nov 2009, 11:49
-
 par axel031 » 01 Nov 2009, 12:45
par axel031 » 01 Nov 2009, 12:45
Oui oui je comprends ca mais ca prouve seulement l encadrement de la 2 eme question ... ;)ab - a > 0 donc ;)ab > a
et b - ;)ab > 0 donc b > ;)ab
on obtient b > ;)ab > a
Mais comment démontres-tu que ;)ab est plus proche de a que de b ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 12:47
par Ericovitchi » 01 Nov 2009, 12:47
Tu veux démontrer que

?
Mets tous les termes d'un seul coté et repère un carré parfait (qui sera donc toujours positif)
-
axel031
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Nov 2009, 11:49
-
 par axel031 » 01 Nov 2009, 13:00
par axel031 » 01 Nov 2009, 13:00
ah oui je comprends mieux mais ou cela nous mène-t-il ?
;)ab - a > b - ;)ab
2;)ab - a - b > 0

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 13:09
par Ericovitchi » 01 Nov 2009, 13:09
Plutôt

< 0
mais
^2)
c'est là qu'il fallait reconnaître l'identité remarquable (x²+y²-2xy=(x-y)²
-
axel031
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Nov 2009, 11:49
-
 par axel031 » 01 Nov 2009, 13:11
par axel031 » 01 Nov 2009, 13:11
Oui je comprends merci beaucoup pour ton aide ! a bientot

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Nov 2009, 13:17
par Ericovitchi » 01 Nov 2009, 13:17
Attention je vois que l'on démontre le contraire

?
équivalent à

ou
(
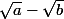^2 <0)
ce qui est faux
donc
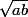
est plutôt plus près de a que de b
-
axel031
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Nov 2009, 11:49
-
 par axel031 » 01 Nov 2009, 13:19
par axel031 » 01 Nov 2009, 13:19
Oui oui j'avais vu mais je peux aussi l'introduire dans ma réponse comme argument en plus ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
