Probleme de limites

par **melanie76000** » 15 Sep 2007, 14:00

Bonjour tout le monde,
je suis en terminale es et
je post un message sur le forum parce que je seche sur un exo de math, j'y suis depuis des heures sans résultats, j'aimerai trouver quelqu'un qui puisse m'expliquer clairement les méthodes. C'est un exercice qui consiste à déterminer des limites et je n'arrive à bout d'aucune

l'exercice en question est le suivant (je ne vous demande pas de me le résoudre, je cherche juste à comprendre ...)

On considère la fonction f définie sur R \ {-3 ; 3} par :

f(x)= (2-x) / (x²-9)

Déterminer les limites f aux bornes de son ensemble de définition.

Comment résoudre une forme indéterminée de la forme infini/infini

et je n'ai pas compris non plus comment utiliser la règle des signes dans une formule de type l / 0 afin de déterminer si la limite est +infini ou -infini

merci de m'aider, je n'en peux plus d'essayer en vain !
je compte sur vous ;)

par **eejit** » 15 Sep 2007, 14:09

pour les limites en + et -

, la méthode est de calculer la limite des monômes de plus haut degré.

Dans ce cas:

Soit

Ca se passe apreil en +

par **melanie76000** » 15 Sep 2007, 14:12

euh...
merci mais je ne comprends pas (jsuis un peu bornée, désolé)

si x tend vers -infini,
comment la limite de -x/x² peut elle etre -1/x

pour moi ca donne +infini/+infini ... :/

par **Minto** » 15 Sep 2007, 14:13

en -3 lim (2-x) = 5 et lim (x² -9) = 0+ ou 0- selon que tu considères x > -3 ou x < -3
si c'est 0+, numérateur et dénominateur positif donc lim f = +l'infini
sinon, - l'infini
pareil pour 3

pour -x/x², tu simplifies juste par x.

par **melanie76000** » 15 Sep 2007, 14:15

et comment je sais si je considère x<-3 ou x>-3 ...:/

par **Minto** » 15 Sep 2007, 14:16

tu dois faire les deux cas!
on te demande les limites aux bornes de l'ensemble, -3 et 3 sont des valeurs interdites, donc tu dois considérer les limites à gauche et à droite de 3 et de -3. (plus celles à l'infini)

par **melanie76000** » 15 Sep 2007, 14:22

donc par exemple si je considère x> -3 ca donne +infini

par **Minto** » 15 Sep 2007, 14:24

non car si x > -3, x² < 9 donc lim (x² - 9) = 0- et lim f = - l'infini. (si j'ai pas fait d'erreur)

par **eejit** » 15 Sep 2007, 14:29

melanie76000 a écrit:euh...
merci mais je ne comprends pas (jsuis un peu bornée, désolé)

ce sont les fonctions qui devraient l'être... :zen:

melanie76000 a écrit:si x tend vers -infini,
comment la limite de -x/x² peut elle etre -1/x

Exemple :

, c'est équivalent à

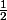
, non?
Simplification par facteurs communs, ça te dit rien?

par **melanie76000** » 15 Sep 2007, 14:33

si si ca me dit bon j'ai le cerveau embrouillé moi

attention je tente (si c'est pas ca jvous previens je vais me suicider)
en 3
si x<3, lim f(x) =+infini ......

par **Minto** » 15 Sep 2007, 14:35

hum oui ça doit être ça, lim (2-x) = -1 et lim (x²-9)=0- à priori.

par **melanie76000** » 15 Sep 2007, 14:37

rah bon ben jme suiciderai ptetre pas encore aujourd'hui alors

bon jvais essayer de ressortir tout ca au clair sur ma feuille
si j'ai un soucis je reviens bien sur ! :zen:

Probleme de limites

Probleme de limites

Qui est en ligne