Problème d'inéquation à résoudre

par **dany** » 14 Sep 2005, 12:57

qui peut m'aider à résoudre cette inéquation? merci par avance et comme toujours c'est urgent!
racine carrée de X - 5 > 1 - X

par **S@m** » 14 Sep 2005, 13:00

Pas besoin de le poster a deux endroits a la fois! . Mais bon... Moi je ferai passer 1-x a gauche et j'utiliserai la quantité conjuguée :marteau: Voila, Amicalement...

par **Anonyme** » 14 Sep 2005, 13:04

dany a écrit:qui peut m'aider à résoudre cette inéquation? merci par avance et comme toujours c'est urgent!
racine carrée de X - 5 > 1 - X

alors tu fais passer -x de l'autre côter et -5 de l'autres coter ce qui donne

2x>6 donc x>6/2 x>3

par **dany** » 14 Sep 2005, 13:10

Non inscrit a écrit:alors tu fais passer -x de l'autre côter et -5 de l'autres coter ce qui donne

2x>6 donc x>6/2 x>3

hélas mon problème est plus compliqué que cela
il s'agit de RACINE CARREE de X - 5 > 1 - X
merci pour les réponses

par **S@m** » 14 Sep 2005, 13:25

Oui mais c'est bien ce que je te dis...tu fais passer (x-5) de l'autre coté et tu utilse la quantité conjuguée...tu sais ce que sais?
Autre question tu a vu les trinomes?

par **rene38** » 14 Sep 2005, 13:37

Bonjour

Est-ce bien

?

par **dany** » 14 Sep 2005, 13:40

rene38 a écrit:Bonjour

Est-ce bien ?

oui c'est bien celà et je ne sai s pas ce que sont les quantités conjuguées merci (nb : il s'agit bien de RACINE CARREE de X - 5 mais je ne sais pas quelles touches utiliser pour taper ce sigle ) merci pour la suite

par **dany** » 14 Sep 2005, 13:50

S@m a écrit:Oui mais c'est bien ce que je te dis...tu fais passer (x-5) de l'autre coté et tu utilse la quantité conjuguée...tu sais ce que sais?
Autre question tu a vu les trinomes?

hélas je suis en 1ère S et je ne connais ni la quantité conjuguée ni les trinomes pouvez-vous poursuivre votre assistance merci par avance pour le temps donné

par **S@m** » 14 Sep 2005, 13:53

Tu n'a pas répondu a ma seconde question, mais je peux au moins t'en dire plus sur ce que moi j'aurai fait...

tu a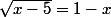

Tu fais passer le (1-x) de l'autre coté ce qui donne:

Tu utilise la suantité conjuguée a celle si, c'est a dire que lorsque tu va les multiplier ensemble tu obtiendra une forme (a+b)(a-b) ou l'inverse soit a²-b².
Ici la forme conjuguée est

donc on a si tu multiplie par ceci des deux cotés:

Donc ce qui donne grace a a²-b²...

donc tu a -x²+3x-6

il te suffit d'etudier le signe du trinome..sauf erreur...

Amicalement

par **rene38** » 14 Sep 2005, 14:05

Je suppose qu'on travaille dans

n'existe que si

c'est à dire

or dans ce cas,

et donc

Le premier membre est positif (c'est une racine carrée) et le second est strictement négatif (inférieur à -4)

Donc

est vrai quel que soit

L'ensemble des solutions est

par **rene38** » 14 Sep 2005, 14:14

s@m >> Attention !

Pense au domaine de définition avant tout calcul.
Quand tu multiplies les 2 membres d'une inéquation par un même nombre,
regarde si ce nombre est positif ou négatif (dans ce dernier cas, changement de sens de l'inéquation)
Dans ton dernier calcul, erreur de transcription (signe moins devant x²)

Cordialement
René

par **S@m** » 14 Sep 2005, 14:22

J'ai corrgié pour le signe moins tout de suite après avoir posté, en relisant...je comprends ce que tu veux dire pour le signe mais escque cela signifie que cette methode est inexacte? :happy2:
Amicalement,

par **dany** » 14 Sep 2005, 14:22

S@m a écrit:Tu n'a pas répondu a ma seconde question, mais je peux au moins t'en dire plus sur ce que moi j'aurai fait...

tu a

Tu fais passer le (1-x) de l'autre coté ce qui donne:
Tu utilise la suantité conjuguée a celle si, c'est a dire que lorsque tu va les multiplier ensemble tu obtiendra une forme (a+b)(a-b) ou l'inverse soit a²-b².
Ici la forme conjuguée est donc on a si tu multiplie par ceci des deux cotés:

Donc ce qui donne grace a a²-b²...

donc tu a -x²+3x-6 il te suffit d'etudier le signe du trinome..sauf erreur...

Amicalement

ta réponse x2 +3x-6>0 je l'avais trouvé mais je n'étais pas sûr de la validité
par contre peux - tu me donner des pistes pour étudier le signe du trinome
merci beaucoup pour ta gentillesse qui me semble aussi infinie que l'univers :we:

par **rene38** » 14 Sep 2005, 14:33

s@m >> "Est-ce que cela signifie que cette méthode est inexacte ?" OUI
** (x-5) DOIT être positif pour que sa racine carrée existe : il faut l'écrire
*** Quand tu multiplies par la quantité conjuguée, tu conserves le sens de l'inéquation sans tenir compte du fait que cette fameuse quantité dépend de x et peut donc être négative.
** et *** entraînent une inéquation finale fausse (elle n'a aucune solution)

par **S@m** » 14 Sep 2005, 14:38

dany a écrit:merci beaucoup pour ta gentillesse qui me semble aussi infinie que l'univers :we:

Comme toute celle de ceux qui repondent ici ^^
Malheuresement rené38 a raison cette methode est fausse car je n'ai pas distingué les signes que pouvait prendre la quantité conjuguée :stupid_in :stupid_in
Il ne te reste donc que la methode de rené38 qui est, je suis sure, la meilleure :briques:

Mea culpa :hum:

par **rene38** » 14 Sep 2005, 14:42

j'ajoute que chercher le signe de la quantité conjuguée revient à résoudre l'inéquation ... on n'en sort pas !

Problème d'inéquation à résoudre

problème d'inéquation à résoudre

Qui est en ligne