Je suis élève en classe de Seconde et j'ai à réaliser avec un ami un exercice qui nous pose plusieurs soucis et dont voici l'énoncé :
Monsieur Farfelu possède un champ de forme triangulaire et une chèvre Caprice qui n'a envie de brouter que dans un enclos rectangulaire.
Illustration du problème :
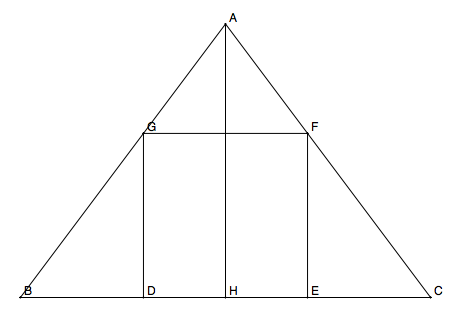
Avec : BC = 12 m
HC = 4 m
HA = 6 m
HB = 8 m
A quelle distance de A, Monsieur Farfelu doit-il planter son premier piquet M pour que sa chèvre Caprice dispose du plus grand espace possible.
Donc pour résoudre le problème on nomme x le segment BD, ce qui permet grâce aux théorème de Thales de calculer DG = 6/8 x dans les triangles BDG et BHA.
Par la suite on fait la même chose pour calculer CE = 1/2 x dans les triangles CFE et CHA.
Jusque là nous nous en sommes tirés mais ensuite, notre professeur nous a indiqué qu'il fallait rechercher DE et que nous devions parvenir au résultat De = 12-3/2 x. Malheureusement le calcul DE = HB-BD+HC-CE
= 8-x+4-1/2x
nous donne bien DE = 12-1/2x
Evidemment nous avons pensé que nous avions faux mais sans parvenir à trouver le résultat indiqué. Donc un premier problème.
De plus, sachant tout de même que DE = 12-3/2x nous avons trouvé l'équation
Aire du champs = 6/8x (12-3/2x)
En l'entrant dans la calculatrice nous avons trouvé comme plus grande valeur de DE possible 4(m) qui donne une aire de 18.
Nous supposons donc que le calcul à réaliser pour prouver qu'il s'agit bien de la plus grande valeur possible de DE est la factorisation de l'expression 6/8x (12-3/2x) -18 mais le développement / simplification du calcul et sa factorisation nous pose également problème.
Je remercie donc d'avance toute âme charitable prête à nous aider rapidement.
Merci.
