Problème Fonction Dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
AllanPoe
- Membre Naturel
- Messages: 95
- Enregistré le: 09 Mar 2013, 16:27
-
 par AllanPoe » 24 Juin 2013, 14:46
par AllanPoe » 24 Juin 2013, 14:46
Luc a écrit:Je ne comprends pas comment tu obtiens cette formule.
Pour moi Pythagore donne R^2=x^2+r^2, où r représente la moitié de la
diagonale du carré.
Et tu sais que dans un carré, le rapport entre une diagonale et un carré vaut

.
Autant pour moi je suis partie dans un autre délire, je trouve bien R^2=x^2+r^2 comme pour les autres
Bon alors moi j'ai trouvé que la moitié d'une diagonale était égale (soit r ) à

10-x)
Donc si on veut avoir la diagonale complète c'est 2(10-x) soit : 20-2x
Ensuite le rapport si je ne me trompe pas c'est :: (diagonale*racine(2))/2
Donc : ((20-2x)*racine(2))/2 non :s ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 24 Juin 2013, 22:40
par Luc » 24 Juin 2013, 22:40
AllanPoe a écrit:Autant pour moi je suis partie dans un autre délire, je trouve bien R^2=x^2+r^2 comme pour les autres
Bon alors moi j'ai trouvé que la moitié d'une diagonale était égale (soit r ) à

10-x)
Non, Pythagore te donne
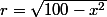
-
AllanPoe
- Membre Naturel
- Messages: 95
- Enregistré le: 09 Mar 2013, 16:27
-
 par AllanPoe » 25 Juin 2013, 00:28
par AllanPoe » 25 Juin 2013, 00:28
Luc a écrit:Non, Pythagore te donne
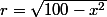
Voyons voir, alors moi j'ai trouvé donc que : côté = (diagonale*2)/racine(2)
Donc ca donne (4*racine(100-x^2))/racine(2)
Donc le côté au carré = 400-4x^2
La formule du volume finale ca sera étant donnée que h=2x
2x(400-4x^2) Je trouve pas du tout la même chose je comprends pas :mur:
-
AllanPoe
- Membre Naturel
- Messages: 95
- Enregistré le: 09 Mar 2013, 16:27
-
 par AllanPoe » 25 Juin 2013, 00:31
par AllanPoe » 25 Juin 2013, 00:31
Black Jack a écrit:A partir du dessin fait avant :
Pour le cône :
h = OS + OO' (avec h la hauteur du cône)
h = 10 + OO'
OO' = (h-10)
O'A² = OA² - OO'²
r² = 100 - (h-10)² (avec r le rayon de la base du cône)
r² = 100 - (h² - 20h + 100) = 20h - h²
Volume du cône : V = (Pi/3).(20h - h²).h
V = (Pi/3).h²(20 - h) (avec h dans [0 ; 20])
*****
Pour le cylindre :
hauteur du cylindre h et rayon de base du cylindre r :
(h/2)² + r² = R²
r² = 100 - h²/4
V = Pi.r².h
V = Pi.(100 - h²/4).h (avec h dans [0 ; 20])
*****
:zen:
Merci

Mais là vu ou en est ma tête je préfère pas m'embrouiller et garder mon inconnue
-
Black Jack
 par Black Jack » 25 Juin 2013, 09:19
par Black Jack » 25 Juin 2013, 09:19
AllanPoe a écrit:Merci

Mais là vu ou en est ma tête je préfère pas m'embrouiller et garder mon inconnue
Tu peux effectivement garder ton inconnue ... bien que je ne la trouve pas la meilleure.
Elle est sûrement bonne mathématiquement et permet de faire les calculs mais elle n'a pas le même sens "physique" dans les 3 cas. Et ce n'est pas idéal pour "sentir" les résultats.
Par contre h (hauteur de la fusée) comme inconnue permet des calculs aussi faciles et a la même signification "physique" dans les 3 cas.
La hauteur de la fusée est quelque chose de bien concret, qu'on "voit avec ses yeux" sur les 3 engins, alors que le x choisi ...
Mais ce n'est que mon avis.
:zen:
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 25 Juin 2013, 10:14
par Luc » 25 Juin 2013, 10:14
AllanPoe a écrit:Voyons voir, alors moi j'ai trouvé donc que : côté = (diagonale*2)/racine(2)
Attention, c'est côté = diagonale * racine(2)/2 (le côté est plus petit que la diagonale).
Et on peut toujours utiliser la factorisation 100-x^2=(10-x)(10+x) comme dans le cas du cylindre.
-
AllanPoe
- Membre Naturel
- Messages: 95
- Enregistré le: 09 Mar 2013, 16:27
-
 par AllanPoe » 26 Juin 2013, 00:17
par AllanPoe » 26 Juin 2013, 00:17
Ouuuuuai ! Merci j'ai bien réussis à trouver
4x(10-x)(10+x) !
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 26 Juin 2013, 11:41
par Luc » 26 Juin 2013, 11:41
AllanPoe a écrit:Ouuuuuai ! Merci j'ai bien réussis à trouver
4x(10-x)(10+x) !
Bravo pour ta persévérance :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
.
