Problème dérivé de fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Paella
- Membre Naturel
- Messages: 34
- Enregistré le: 25 Sep 2006, 18:23
-
 par Paella » 24 Fév 2007, 20:39
par Paella » 24 Fév 2007, 20:39
Bonsoir comme l'intitule le sujet j'ai un problème sur les dérivés de fonction et je bloque des la premiere question je vous la présente si dessous :
Soit f la fonction définie sur R\2 par f(x) = x²-x+2/x-2
1. Déterminer les réels a, b, c tels que : f(x)= ax+b+ c/x-2
Si quelqun peut m'expliquer comment faire je vous en serais reconnaisant merci de votre aide
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 24 Fév 2007, 20:46
par nxthunder » 24 Fév 2007, 20:46
f(x) = x²-x+é/x-2
Est ce cela ?
 = x^2-x +\frac{2}{x-2})
ou bien
 = \frac{x^2-x+2}{x-2})
?
Sinon la méthode à appliquer est une identification des membres de meme degré.
-
Paella
- Membre Naturel
- Messages: 34
- Enregistré le: 25 Sep 2006, 18:23
-
 par Paella » 24 Fév 2007, 20:53
par Paella » 24 Fév 2007, 20:53
c'est ta deuxième fonction qui est la bonne escuse moi de la faute, et pour identifier les membres on a un x² dans la premiere fonction donc je vois pas trop comment faire
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 24 Fév 2007, 21:41
par MacErmite » 24 Fév 2007, 21:41
Bonsoir ,
j'ai essayé de travailler sur ton problème et voilà comment j'ai procédé ...
tout d'abord j'ai posé la division
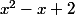
par
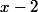
(comme les divisions avec des nombres) on a alors (x-1) et il reste 2x soit :
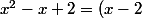(x-1)+2x)
Je pose ensuite :
(x-1)+2x \\<br />\frac{x^2-x+2}{x-2}&=&\frac{(x-2)(x-1)}{x-2}+\frac{2x}{x-2}\\<br />\frac{x^2-x+2}{x-2}&=&(x-1)+\frac{2x}{x-2}<br />\end{eqnarray})
j'espére que cela va t'aider.
-
Paella
- Membre Naturel
- Messages: 34
- Enregistré le: 25 Sep 2006, 18:23
-
 par Paella » 24 Fév 2007, 21:44
par Paella » 24 Fév 2007, 21:44
oui merci je pense que ça va m'aider merci je vois deja mieux comment il faut s'y prendre
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 24 Fév 2007, 22:04
par MacErmite » 24 Fév 2007, 22:04
Oui enfin c'est pas exactement la forme recherchée, zut.
alors si on pose :
(x-2)}{x-2}+\frac{c}{x-2}\\<br />\frac{x^2-x+2}{x-2}&=&\frac{ax^2-2ax+bx-2b+c}{x-2}<br />\end{eqnarray})
Après on identifie :
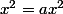
donc a=1;
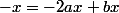
donc b=1;
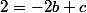
donc c=4;
Ce qui fini par donner :
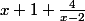
-
Paella
- Membre Naturel
- Messages: 34
- Enregistré le: 25 Sep 2006, 18:23
-
 par Paella » 25 Fév 2007, 14:08
par Paella » 25 Fév 2007, 14:08
Merci de ton aide maintenant on me demande de deriver la fonction f dois-je reprendre la formule de départ ou celle çi ?
-
Paella
- Membre Naturel
- Messages: 34
- Enregistré le: 25 Sep 2006, 18:23
-
 par Paella » 25 Fév 2007, 14:24
par Paella » 25 Fév 2007, 14:24
Si on reprend la dernière formule on obtient 1+ -4/(x-2)²
Et si on prend la premiere on obtient : (2x-1)(x-2)-(x²-x+2)/(x-2)²
: 2x²-2x-x-2-x²-x+2/(x-2)²
: x²-4x/(x-2)²
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 25 Fév 2007, 14:31
par MacErmite » 25 Fév 2007, 14:31
Je viens de vérifier :
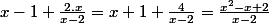
du coup tu prends celle qui te parait la plus simple à dériver. Mais tu es guidé apparemment par les questions précédentes.
avec la forme n°2, qui me paraît la plus facile, cela donne :
^2})
. Mais sache qu'elles donnent toutes le même résultat.
-
Paella
- Membre Naturel
- Messages: 34
- Enregistré le: 25 Sep 2006, 18:23
-
 par Paella » 25 Fév 2007, 14:33
par Paella » 25 Fév 2007, 14:33
Ok je vais faire comme ça
-
Paella
- Membre Naturel
- Messages: 34
- Enregistré le: 25 Sep 2006, 18:23
-
 par Paella » 25 Fév 2007, 14:45
par Paella » 25 Fév 2007, 14:45
Ok donc c'est bien ce que j'avais trouvé je dois maintenant étudier le signe de f '(x), les valeurs que je dois metre dans mon tableau sont 1 et 4/(x-2)² ou -4/(x-2)² ?
-
Paella
- Membre Naturel
- Messages: 34
- Enregistré le: 25 Sep 2006, 18:23
-
 par Paella » 25 Fév 2007, 15:04
par Paella » 25 Fév 2007, 15:04
Donc j'ai dressé mon tableau de signe avec 1 et -4/(x-2)² dedans et j'arrive a quelque chose comme quoi la variation de f serai décroissante entre - l'infini ~ 0 et 0 ~ + l'infini alors que ce n'est pas le cas
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 25 Fév 2007, 15:14
par MacErmite » 25 Fév 2007, 15:14
Je viens de faire un tableau de variation, mais cela fait plus d'une décennie que j'en ai pas fait, alors tu devras le vérifier

-
Paella
- Membre Naturel
- Messages: 34
- Enregistré le: 25 Sep 2006, 18:23
-
 par Paella » 25 Fév 2007, 15:18
par Paella » 25 Fév 2007, 15:18
Merci, je l'ai fait avec la fonction qu'on donne au début ça donne la même chose :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités

