Problème construction d'un triangle, besoin de piste...

[Liee-x3]

Bonjour, mon enoncé est :
"Construire un triangle ABC tel que AB=4 cm, AC=5 cm et dont l'aire vaut 9 cm²"
Je ne trouve pas la méthode pour construire ce triangle, si vous avez des idées ...

[maturin]

dessine un triangle quleconque pour commencer.
appelle H le pied de la hauteur venant de A.
appelle ensuite:
h=AH
x=BH
y=HC

pytagore dans AHB
(E1) h²+x²=AB²=16
pytagore dans AHC
(E2) h²+y²=25

Cas 1: H sur [BC]
(E3) aire de ABC=aire de ABH+aire de AHC=(xh/2)²+(yh/2)²=9

Cas 2: H en dehors de [BC] (du côté de B car AB(E3bis) aire de ABC=aire de ACH-aire de ABH=(yh/2)²-(xh/2)²=9

Ce qui te fais 3 équations à 3 inconnues, et deux cas à traiter.
Trouves les solutions et trace ton / tes triangles possibles.

[Liee-x3]

D'accord ! Merci beaucoup pour ton aide :)

[Liee-x3]

Oui. Là j'essaye de faire mes calculs mais je suis complètement perdue :mur:

[maturin]

j'avoue que je trouve ça assez naze comme exo surtout que ca tombe pas forecement juste (j'ai aps fait les calculs mais ça m'a l'air pouri)

[Liee-x3]

Lol ! Moi pauvre petite tête qui cherche à le faire depuis 15h30 je n'ai pas avancé d'un poil ! C'est soi impasse, soi on ne connait pas les méthodes.

[maturin]

Cas 1: H sur [BC]
(E3) aire de ABC=aire de ABH+aire de AHC=(xh/2)+(yh/2)=9

Cas 2: H en dehors de [BC] (du côté de B car AB<AC)
(E3bis) aire de ABC=aire de ACH-aire de ABH=(yh/2)-(xh/2)=9

Comme tu l'auras surement noté j'ai fait une erreur dansles aires il n'y a pas les ²

Ce qui bien entendu rend les calculs encore plus compliqués...

[Liee-x3]

Oui je l'ai vu mais je n'en ai pas tenu compte. Cette exercice a le dont de m'exaspérer. La solution est surement toute bête mais pour la trouver c'est une autre histoire !

[Liee-x3]

J'ai résolu l'exercice. J'ai simplement cherché 2hauteurs pour construire ma figure. Après je pense que cet exercice est une question de point de vue, avec plusieurs méthodes.
Merci à tout le monde de m'avoir aidé :)
Bonne soirée !

[Timothé Lefebvre]

cet exercice est une question de point de vue, avec plusieurs méthodes.

Bonsoir,

oui c'est sûr, Héron était utilisable comme on te l'a dit n'est-ce pas ...

Mais bien entendu c'est une question de point de vue comme l'a très bien dit mon collègue.

[maturin]

la solution est toute bete si l'aire était de 10cm² (i.e. triangle rectangle en A)

là dans le cas 1 je trouve:

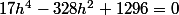
Soit une équation du second dégré en h²
Ce qui donne deux solution pour h, x et y

Ce qui fait 2 possibilités avec BC=4.854 ou BC=7.644

J'ai pas fait les calculs avec les expressions exactes jusqu'au bout...

[maturin]

bon je viens de voir la réponse avec le dessin des hauteurs, c'est vrai c'est bcp plus simple :) comme quoi réfléchir avant de faire des calculs bourrin c'est pas mal...