Un problème avec une limite

[Lord Kira]

Salut tous le monde .
Voilà j'ai un problème avec une limite que j'ai pas réussi a résoudre .
là voilà :



Merci de me dire la méthode .

merci encore .

[anima]

Salut tous le monde .
Voilà j'ai un problème avec une limite que j'ai pas réussi a résoudre .
là voilà :



Merci de me dire la méthode .

merci encore .

J'ai le droit a quels outils?

[chan79]

on peut bien le faire avec un développement limité de tan x
tan(x)= x + x^3/3 + 2*x^5/15 + 17*x^7/315 +...
et la limite est 0
ce n'est peut-être pas ce qui est attendu ici ...

[Lord Kira]

J'ai le droit a quels outils?

bah tu peux faire tous ce que tu veux .

on peut bien le faire avec un développement limité de tan x
tan(x)= x + x^3/3 + 2*x^5/15 + 17*x^7/315 +...
et la limite est 0
ce n'est peut-être pas ce qui est attendu ici ...

Bah j'ai rien compris là peux tu expliquer ?

merci

[le_fabien]

on a donc (tanx-x)/(x-0)*(1/x) cela fait penser à un taux d'accroissement multiplié à 1/x

[le_fabien]

j'ai même une meilleure ecriture:
(tanx-x)/x^2=((tanx)/x-1)/x
en posant f(x)=tanx/x avec f(0)=1 (cf cours)
cette limite est égale à f'(0)

[Nightmare]

Salut Lefab11 :happy3:,

encore faut-il f'(0) existe !

[le_fabien]

Salut nightmare
f(o) existe grâce à la limite en 0 de sinx/x
et on a tanx/x=(1/cosx)*(sinx/x) qui admet une limite en 0

[le_fabien]

puis 1/cosx est dérivable en 0 et aussi sinx/x

[anima]

puis 1/cosx est dérivable en 0 et aussi sinx/x

tan(x)/x^2 - 1/x. Si c'était que tanx/x,y'aurait tres peu de problemes...

[le_fabien]

en résumé pour moi :
f(x)=tanx/x et f dérivable en 0 car elle est produit de deux fonctions dérivables en 0 d'où lim en 0 ((f(x)-f(0)/(x-0)) = lim en 0 ((tanx/x-1)/x)=lim en 0 (tanx-1)/x^2=f'(0)=0
si une personne pouvait me dire si mon raisonnement n'est pas bon.merci

[anima]

en résumé pour moi :
f(x)=tanx/x et f dérivable en 0 car elle est produit de deux fonctions dérivables en 0 d'où lim en 0 ((f(x)-f(0)/(x-0)) = lim en 0 ((tanx/x-1)/x)=lim en 0 (tanx-1)/x^2=f'(0)=0
si une personne pouvait me dire si mon raisonnement n'est pas bon.merci

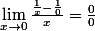
Chez moi, , donc 1/x n'est pas dérivable en zéro. Ce n'est pas parce que la fonction est dérivable partout ailleurs qu'elle le sera en un point singulier.

[le_fabien]

salut anima
je n'ai jamais énoncé que 1/x était dérivable en O mais je parle de (tanx)/x qui elle est dérivable en 0

[anima]

salut anima
je n'ai jamais énoncé que 1/x était dérivable en O mais je parle de (tanx)/x qui elle est dérivable en 0

Moi aussi, je parlais de ca. Ta démonstration rapide de cette propriété manque de rigeur. Ce n'est pas parce que tan(x) est le produit de 2 fonctions dérivables en zéro qu'elle (et par la suite tanx/x) est dérivable en zéro. C'est parce que:


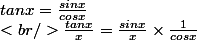
1/cosx->1
sinx/x -> 1.

La voila, la preuve. Et encore, il faut prouver rigoureusement que sinx/x est bien dérivable en zéro a l'aide soit des DL, soit de la trigo.

D'ou . Et la, il faudra vraiment que tu m'expliques comment tu arrives a lever la F.I. de . Car c'est certainement pas avec ce qu'il y a plus haut...

[le_fabien]

je sais que je n'ai pas détaillé mais sinx/x est dérivable en 0
cela se démontre grâce à:
pour tout x>=0 (-x^3)/3<=sinx-x<=0
cette double inégalité ce démontre en dérivant trois fois la fonction h(x)=sinx-x+(x^3)/3...
désolé de ne pas avoir trop détaillé.

[anima]

je sais que je n'ai pas détaillé mais sinx/x est dérivable en 0
cela se démontre grâce à:
pour tout x>=0 (-x^3)/3<=sinx-x<=0
cette double inégalité ce démontre en dérivant trois fois la fonction h(x)=sinx-x+(x^3)/3...
désolé de ne pas avoir trop détaillé.

... T'as pris la démonstration dans le sens inverse et tu l'as totalement charcutée.

Pour toute fonction dérivable n fois en x=0, on peut écrire que avec
Prenons n = 3, on obtient
Il va de soi que, pour x proche de zéro (ou tendant vers zéro),

[lapras]

Tiens je reconnais la les fameuses D.L !
Ca me donne envie d'écrire un programme sur Ti pour les DL, car j'ai vraiment la flemme de dériver la fonction plein de fois