[1ere S] Problème avec une inéquation.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 30 Oct 2009, 21:15
par tite_prune » 30 Oct 2009, 21:15
Bonsoir , me voila encore avec un problème que j'ai essayé de résoudre mais j'arrive vraiment à rien :/
Voici l'énnoncé:
On se propose de résoudre dans IR l'inéquation (I):2x^3-2x²-5x+2>0
-determiner 3 réels a , b et c tels que pur tout x appartenant à IR, on ait : (I)=(x-2)(ax²+bx+c)
donc moi j'ai commencé à developper (x-2)(ax²+bx+c) et j'ai eu ça (x-2)(ax²+bx+c)=ax^3+bx²+cx-2ax²-2bx-2cDonc voila à partir de là je bloque totalement.
J'espère que quelq'un pourra m'aider , merci d'avance .

(Mon post que j'ai crée y'a 5 minutes à surement été supprimer donc si j'ai pu écrire quelque chose d'irrespectueu je m'en excuse)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Oct 2009, 21:25
par Dinozzo13 » 30 Oct 2009, 21:25
Salut, regroupe les termes des différents degrés de ax^3+bx²+cx-2ax²-2bx-2c, les x² avec les x², les x avec les x.
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 30 Oct 2009, 21:32
par tite_prune » 30 Oct 2009, 21:32
Donc il faut que je factorise comme ça :
(x-2)(ax²+bx+c)=ax^3+bx²+cx-2ax²-2bx-2c=ax^3+x²(b-2a)+x(c-2b)-2c
et ensuite il faudrait que je trouve mes vaeurs des nombres a , b et c mais je vois pas la technique pour :soupir2:
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 30 Oct 2009, 21:39
par MacManus » 30 Oct 2009, 21:39
Bonsoir
tite_prune a écrit:(x-2)(ax²+bx+c)=ax^3+bx²+cx-2ax²-2bx-2c=ax^3+x²(a-b)+cx-2c
Non, tu as mal regroupé tes termes en x² et en x (en rouge)
Tu dois obtenir autre chose
x^2 + (....)x -2c)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 30 Oct 2009, 21:40
par MacManus » 30 Oct 2009, 21:40
Ah voilà tu as bien modifié
OK
Maintenant tu identifies les coefficients de ton polynôme de départ et ceux du polynôme que tu viens d'obtenir !
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 30 Oct 2009, 21:42
par tite_prune » 30 Oct 2009, 21:42
Oui je me suis corrigée ^^
(x-2)(ax²+bx+c)=ax^3+bx²+cx-2ax²-2bx-2c=ax^3+x²(b-2a)+x(c-2b)-2c
je crois que c'est bon mais ensuite il faut procédé par identification je crois mais là je sais pas du tout comment faire :/
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 30 Oct 2009, 21:48
par tite_prune » 30 Oct 2009, 21:48
alors attends dans le 1er polynome on a a , b et c et dans le 2eme on a a, b-2a , C-2b , et c , c'est ca?
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 30 Oct 2009, 22:23
par tite_prune » 30 Oct 2009, 22:23
Si y'a quelqu'un qui veut bien m'aider je suis partante ^^
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Oct 2009, 22:34
par Dinozzo13 » 30 Oct 2009, 22:34
Me revoila, procède par identification donc ça équivaut à trouver a,b et c tel que :
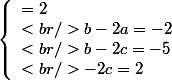
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 30 Oct 2009, 22:38
par tite_prune » 30 Oct 2009, 22:38
Je ne comprend pas (désolée je suis un peu lourde) , pourquoi doit on trouver ces résultats , est ce que je dois moi trouver comment toi tu trouves ces résultats ou par rapport au texte tu les trouve?
--------------
Non j'ai trouv" je crois par rapport a (I) on a a=2 et après on trouve les autre en faisant les soustraction ou addition ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Oct 2009, 22:41
par Dinozzo13 » 30 Oct 2009, 22:41
oui voila, il te suffit juste de calculer a,b et c ^^
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 30 Oct 2009, 22:42
par tite_prune » 30 Oct 2009, 22:42
Aaaaaaaaaa ok !! Merci !!! :we: et après pour résoudre (I) e remplace avec les valeur que j'ai trouvé et ca me donnera un résultat?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Oct 2009, 22:54
par Dinozzo13 » 30 Oct 2009, 22:54
Par conséquent :
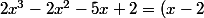(2x^2+2x-1))
Or on veut résoudre

, donc il faut factoriser au maximum pour pouvoir etudier son signe, il faut donc factoriser

, pour cela on résous
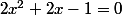
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 30 Oct 2009, 23:08
par tite_prune » 30 Oct 2009, 23:08
Donc on a ici 2 racines vu que le discriminant est égal à 12
et les 2 racines sont x1=(-2-2{racine carrée}3)/4
et x2=(2-2{racine carrée}3)/4
Et donc c'est par ces 2 racines que l'on peut factoriser
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Oct 2009, 23:53
par Dinozzo13 » 30 Oct 2009, 23:53
voilà, ensuite tu fait un tableau de signe et tu en déduis l'ensemble des solutions.
-
tite_prune
- Membre Relatif
- Messages: 163
- Enregistré le: 29 Oct 2009, 13:11
-
 par tite_prune » 31 Oct 2009, 10:43
par tite_prune » 31 Oct 2009, 10:43
Merci beaucoup Dinozzo :D
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 02 Nov 2009, 00:43
par Dinozzo13 » 02 Nov 2009, 00:43
:ptdr: de rien.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
