Problème avec une factorisation

par **jojo0427** » 01 Mai 2009, 15:12

Bonjour à tous je bug sur un petit problème qui me semble très simple mais auquel je n'arrive pas à trouver la solution. Voila mon problème

Je dois factoriser y= (jLW/jRLW)+(R/jRLW)-(RLCW²/jRLW)

Je vous épargne les simplifications que je juge bonne et j'obtient au final

y= (1/R)+(1/jLW)-(CW/j)

Je suis proche de la solution mais je n'y arrive pas sachant que le résultat final doit être y= (1/R)+j[CW-(1/LW)]

J'espère que quelqu'un pourra m'aider sur ce petit problème. Merci

par **bombastus** » 01 Mai 2009, 15:16

Bonjour,

tu es très proche en effet.
As-tu essayé de factorisé par j les 2 derniers termes?

par **jojo0427** » 01 Mai 2009, 15:21

Quand je factorise cela me donne

y= (1/R)+(1/j)[(1/(LW))-CW))]

mais je sais que c un truc vraiment tous bête xD mais je sais pas je suis bloqué à ce niveau

par **bombastus** » 01 Mai 2009, 15:39

Non, je t'ai dit de factoriser par j, et non pas par 1/j!

par **jojo0427** » 01 Mai 2009, 15:54

quand je factorise par j cela me donne y= (1/R)+j[(1/(LW))-CW)]

par **Cheche** » 01 Mai 2009, 15:55

Vu le résultat, je pense que ton j est le i complexe, non ??

par **bombastus** » 01 Mai 2009, 15:56

Ca ne te semble pas bizarre de trouver la même en factorisant par j et par 1/j??

Ton dernier résultat est faux...

Cheche a écrit:Vu le résultat, je pense que ton j est le i complexe, non ??

Oui, c'est la notation utilisé en électronique (pour ne pas confondre avec l'intensité, je crois)

par **jojo0427** » 01 Mai 2009, 16:07

oui c'est bien un complexe. Franchement je vois pas comment factoriser à part donner le bon résultat directement. Mais je ne comprends pas comment on fait je suis trop nul je crois :cry:

par **bombastus** » 01 Mai 2009, 16:14

Mais non, ne te décourage pas!

Par exemple a+2 = a(1+2/a)

par **Cheche** » 01 Mai 2009, 16:38

Je te rappelle que

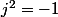
Peut-être utile pour tes problèmes de 1/j et j ?

par **Seekname** » 01 Mai 2009, 16:46

Avec les propriétés citées précédemment, tu devrais trouver.
1 )

2 ) j² = -1

par **jojo0427** » 01 Mai 2009, 17:31

ok mais pour a+b= a(1+(b/a)) que représente a et b pour

y= (1/R)+(1/(jLW))-((LW)/j))

a= 1/R

b= (jLW))-((LW)/j))

??

par **bombastus** » 02 Mai 2009, 13:10

Nous t'avons donné les règles de calcul nécessaires à la résolution de ton problème, ce sont des règles générales, tu ne dois pas forcément chercher une correspondance directe...

Par exemple on aurais pu écrire (pour être plus proche de ton calcul) : a+b = j(a/j+b/j)

Maintenant essaie de factoriser (1/(jLW))-((LW)/j))
tu dois obtenir j(........)

(et pour vérifier, quand tu redéveloppes ton j dans la parenthèse, tu dois retomber sur l'expression initiale)

Problème avec une factorisation

Problème avec une factorisation

Qui est en ligne