Problème avec une démonstration
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
qelmcpc
- Membre Naturel
- Messages: 72
- Enregistré le: 07 Avr 2014, 18:23
-
 par qelmcpc » 12 Juil 2015, 13:10
par qelmcpc » 12 Juil 2015, 13:10
Bonjour,
J'ai un problème avec la démonstration du lemme suivant:
Soit des entiers a, b et i. Si on a
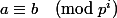
alors
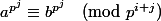
pour tout entier j
Il faut démontrer le cas j = 1, ce qui est OK, mais j'ai un problème pour faire la récurrence...
Je ne vois pas comment passer de j à j+1 en assurant la congruence mod p^i+j+1
Merci beaucoup
-
M.Floquet
- Membre Naturel
- Messages: 54
- Enregistré le: 22 Juin 2014, 14:14
-
 par M.Floquet » 13 Juil 2015, 15:02
par M.Floquet » 13 Juil 2015, 15:02
Résultat bizarre

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Juil 2015, 22:39
par Ben314 » 13 Juil 2015, 22:39
Salut,
Si
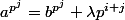
avec
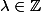
alors
^p = \Big(b^{p^j}+ \lambda p^{i+j}\Big)^p<br />=\sum_{k=0}^p{p\choose k}\Big(\lambda p^{i+j}\Big)^k \Big(b^{p^j}\Big)^{p-k})
et "l'astuce" consiste à voir que le coeff. binomial
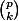
est divisible par
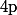
pour tout
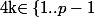
donc
^k\equiv 0\ [p^{i+j+1}]\)
pour tout
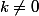
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
M.Floquet
- Membre Naturel
- Messages: 54
- Enregistré le: 22 Juin 2014, 14:14
-
 par M.Floquet » 14 Juil 2015, 01:06
par M.Floquet » 14 Juil 2015, 01:06
Bien vu !!!
Sinon c'est inexploitable, j'avais essayé la formule du binôme sur (j+1)^p mais sans grand succès ...
-
qelmcpc
- Membre Naturel
- Messages: 72
- Enregistré le: 07 Avr 2014, 18:23
-
 par qelmcpc » 14 Juil 2015, 12:30
par qelmcpc » 14 Juil 2015, 12:30
Ben314 a écrit:Salut,
Si
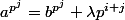
avec
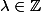
alors
^p = \Big(b^{p^j}+ \lambda p^{i+j}\Big)^p<br />=\sum_{k=0}^p{p\choose k}\Big(\lambda p^{i+j}\Big)^k \Big(b^{p^j}\Big)^{p-k})
et "l'astuce" consiste à voir que le coeff. binomial
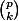
est divisible par
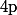
pour tout
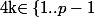
donc
^k\equiv 0\ [p^{i+j+1}]\)
pour tout
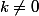
merci beaucoup!
cela m'a donné une autre idée (au lieu de regarder le coef. binomial, on regarde le terme avec le lambda):
on peut dire que si k>= 2 alors k(i+j) >= i+j+1 donc on a bien 0 mod p^(i+j+1) quand k >= 2. Il nous reste k=1 et k= 0. Avec k = 1 on a bien un truc qui vaut 0 mod p^(i+j+1) car
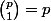
et on a p*p^(i+j) = p^i+j+1 Donc il nous reste k =0 et ça donne bien le terme avec la puissance de b.
C'est correct?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Juil 2015, 07:17
par Ben314 » 15 Juil 2015, 07:17
Oui, c'est parfaitement correct et même plus élémentaire.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
