Problème avec le logarithme népérien

[jenaimarre]

bonsoir a tous je viens a vous car j'ai un dm de math a rendre et je suis un peu bloquer a un exercice c'est une question ouverte avec le logarithme népérien
On note T la courbe de la fonction ln dans un repère (0;i;j) orthonormé, et M un point de T.
Déterminer le ou les points M tel(s) que la distance OM soit minimale.

J'ai quelques idées mais appart faire la dérive le tableau de signe étudier le sens de variation (sauf qu'on sait que la fonction logarithme népérien est toujours croissante) et évaluer le maximum je ne sais pas trop quoi faire si vous auriez quelques pistes pour m’éclaircir.
Merci!! :hein:

[Lostounet]

Le point M a pour coordonnées M(x ; ln(x)) vu qu'il appartient à la courbe T.
Le point O a pour coordonnées O (0; 0).

Que vaut la distance OM en fonction de x?

OM² = x^2 + ln^2(x)

[mathelot]

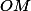
atteint son minimum si et seulement si atteint son minimum

il s'agit donc d'étudier les variations de

[Lostounet]

Tiens mathelot, comment pourrait-on résoudre ln(x) + x² = 0?

[toctoc]

je ne comprends pas pourquoi on est obligé de mettre au carré la distance OM ?

[jenaimarre]

Je ne comprends pas pourquoi on est obligé de mettre au carré la distance OM ?

[mathelot]

Tiens mathelot, comment pourrait-on résoudre ln(x) + x² = 0?

je fais tourner la méthode de Newton



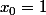
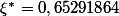
est l'abscisse du point M qui réalise le minimum de

[jenaimarre]

Ah surement pour enlever la racine non ? sinon on aurait OM=;) ((lnx)^2+x^2) non ?

[jenaimarre]

je fais tourner la méthode de Newton

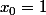
Le probleme mathelot c'est que je n'ai jamais vu ça en cours ???

[mathelot]

fais une dichotomie , à ce moment là

[jenaimarre]

fais une dichotomie , à ce moment là

Est ce que tu crois que je peux mettre
(ln(x))^2=-x^2
par contre je peux pas faire la racine je vais essayer avec le théorème des valeurs intermédiaire par contre comment je pourrais procéder pour faire le tableau de variations ?