bonjour tout le monde.J'ai presque fini un devoir a remettre a la rentree mais il y a toujours deux questions qui me posent problemes.J'aimerais beaucoup me faire aider mais en ayant la demarche explicative svt
Voici les fonctions soit la fonction f definie sur IR par f(x)=1-4(x+1)^2 et g(x)=2x+1
Soit C la courbe representant la fonction f dans un repere orthonormal
Comment faire pour determiner les points d'intersection de C avec l'axe des abscisses? pareil pour le point d'intersection entre C et l'axe des ordonnees.
faut il utiliser une inequation ou une equation?!
comment demontrer que f(x)-g(x)=-4(x+2)(x+1/2)
parce que moi je trouve que f(x)-g(x)=1-4(x+1)^2-2x+1
= -4x^2-8x-3-2x-1
mais apres je ne vois pas trop quoi faire
et je sais que ca peut paraitre facil mais je n'arrive pas trop a determiner le sens de variation de la fonction sur l'intervalle ]-l'infini;-1] et sur [-1;+l'infini[
j'attends votre aide svp
Probleme avec les fonctions
2 messages
- Page 1 sur 1
Salut,
**
-g(x)=1-4(x+1)^2-2x+1=-4(x^2+2x+1)-2x)
Donc-g(x)=-4x^2-8x-4-2x=-4x^2-10x-4)
Or,(x+\frac{1}{2})=-4(x^2+\frac{5x}{2}+1)=-4x^2-10x-4)
Conclus.
(tu peux être plus rapide avec la méthode du discriminant mais je ne sais pas si tu l'as vu)
**Comment faire pour determiner les points d'intersection de C avec l'axe des abscisses?
Il suffit de résoudre=0)
**pareil pour le point d'intersection entre C et l'axe des ordonnees
=...)
**et je sais que ca peut paraitre facil mais je n'arrive pas trop a determiner le sens de variation de la fonction
De quelle(s) fonction(s) parles-tu ?
La fonction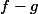 ,
,  ou
ou  ?
?
A+
**
Donc
Or,
Conclus.
(tu peux être plus rapide avec la méthode du discriminant mais je ne sais pas si tu l'as vu)
**Comment faire pour determiner les points d'intersection de C avec l'axe des abscisses?
Il suffit de résoudre
**pareil pour le point d'intersection entre C et l'axe des ordonnees
**et je sais que ca peut paraitre facil mais je n'arrive pas trop a determiner le sens de variation de la fonction
De quelle(s) fonction(s) parles-tu ?
La fonction
A+
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
