Probleme avec GeoGebra

[Clemo]

Bonjour, je suis sur un exercice avec le logiciel GeoGebra et je n'arrive pas a construire un certain point. Pour que vous compreniez je met le début de l'exercice:
- Construire le point A(-1;0) ;) pas de problème
- Construire le point B(b;0) ;) pas de problème
- Le demi-cercle de diamètre [AB] situé au dessus de l'axe des abscisses, intercepte l'axe des ordonnées au point C ;) J'ai construis le demi-cercle et le point C
- Le point M a la même abscisse que le point B et la même ordonnée que le point C ;) C'est la que je bloque je sais pas comment "dire" au logiciel "même ordonnée que le point C" en gros la question est que mettre au niveau du point d’interrogation: M(b;?)

J'espère que vous avez compris ma question et que vous allez m'aider en tous cas merci d'avance

[titine]

Bonjour, je suis sur un exercice avec le logiciel GeoGebra et je n'arrive pas a construire un certain point. Pour que vous compreniez je met le début de l'exercice:
- Construire le point A(-1;0) pas de problème
- Construire le point B(b;0) pas de problème
- Le demi-cercle de diamètre [AB] situé au dessus de l'axe des abscisses, intercepte l'axe des ordonnées au point C J'ai construis le demi-cercle et le point C
- Le point M a la même abscisse que le point B et la même ordonnée que le point C C'est la que je bloque je sais pas comment "dire" au logiciel "même ordonnée que le point C" en gros la question est que mettre au niveau du point d’interrogation: M(b;?)

J'espère que vous avez compris ma question et que vous allez m'aider en tous cas merci d'avance

M=(x(B),y(C))
x(B) désigne l'abscisse du point B

[Clemo]

M=(x(B),y(C))
x(B) désigne l'abscisse du point B

Cela ne marche pas avec le logiciel

[titine]

Cela ne marche pas avec le logiciel

Chez moi si !
J'ai créé un point A.
Puis j'ai saisi B=(x(A),2y(A)) et il m'a bien construit le point B qui a la même abscisse que A et dont l'ordonnée et le double de celle de A.
Bizarre ...

[Joker62]

Hello,

Sinon, on trace deux perpendiculaires.

[Clemo]

Chez moi si !
J'ai créé un point A.
Puis j'ai saisi B=(x(A),2y(A)) et il m'a bien construit le point B qui a la même abscisse que A et dont l'ordonnée et le double de celle de A.
Bizarre ...

Mais ce n'est pas ce qu'on veut, on veut le point M avec l'abscisse de B et l'ordonnée de C

[Clemo]

Hello,

Sinon, on trace deux perpendiculaires.

Comment ça?

[titine]

Mais ce n'est pas ce qu'on veut, on veut le point M avec l'abscisse de B et l'ordonnée de C

D'accord mais c'était pour tester qu'il comprenait bien x(A) pour l'abscisse de A et y(A) pour l'ordonnée de B. Et y a pas de problème, ça marche !

[titine]

Tu peux aussi tracer une parallèle à l'axe des ordonnées passant par B et une parallèle à l'axe des abscisses passant par C.

[Clemo]

D'accord mais c'était pour tester qu'il comprenait bien x(A) pour l'abscisse de A et y(A) pour l'ordonnée de B. Et y a pas de problème, ça marche !

Je comprend pas ce que t'essaye de me dire

[Clemo]

Tu peux aussi tracer une parallèle à l'axe des ordonnées passant par B et une parallèle à l'axe des abscisses passant par C.

Je crois que c'est ce que je vais faire

[titine]

Je comprend pas ce que t'essaye de me dire

Je veux te dire que Geogebra comprend :
M=(x(B),y(C))
Quel message d'erreur as tu ?

[Clemo]

Je veux te dire que Geogebra comprend :
M=(x(B),y(C))
Quel message d'erreur as tu ?

Ca marche!!!! C'est parce ce je mettait pas le égal après le M!
Merci beaucoup

[titine]

Ca marche!!!! C'est parce ce je mettait pas le égal après le M!
Merci beaucoup

C'est bien ce que je disais !!

[Clemo]

Maintenant, il fait que je détermine les coordonnées du point M en fonction de b (abscisse de B), en utilisant le théorème de Pythagore dans trois triangles rectangles mais je vois pas comment étant donnée que le théorème de Pythagore sert à définir des longueurs....

Quelqu'un pour m'aider?

[chan79]

Maintenant, il fait que je détermine les coordonnées du point M en fonction de b (abscisse de B), en utilisant le théorème de Pythagore dans trois triangles rectangles mais je vois pas comment étant donnée que le théorème de Pythagore sert à définir des longueurs....

Quelqu'un pour m'aider?

la hauteur est moyenne proportionnelle entre les segments qu'elle détermine sur l'hypoténuse

[Clemo]

la hauteur est moyenne proportionnelle entre les segments qu'elle détermine sur l'hypoténuse

Je ne comprends pas ce que tu dis

[chan79]

Je ne comprends pas ce que tu dis

si O est l'origine, tu as OC²=OA.OB

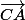
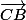
Tu pourrais aussi écrire que le produit scalaire de et est nul.

A noter qu'il devrait y avoir b>0 dans l'énoncé.

[Clemo]

si O est l'origine, tu as OC²=OA.OB

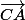
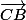
Tu pourrais aussi écrire que le produit scalaire de et est nul.

A noter qu'il devrait y avoir b>0 dans l'énoncé.

Mais il faut ce placer dans trois triangles rectangle or la tu n'est que dans un seul ou je me trompe
On a pas vu le produit scalaire
Oui b est positif

[Ben314]

COB rectangle en O => ...
COA rectangle en O => ...
ABC rectangle en C (pourquoi ?) => ...

donc ...