Bonjour :we:
Je passe le bac de maths jeudi et j'ai un petit probleme avec les probas : comment trouver le nombre total d'éventualités par rapport au systeme étudié.
Par exemple je sais dans le cas d'une urne avec des boules que le nombre totale d'éventualités est égal au nombre de boules. Dans une urne de 6 boules contenant 3 bleues la probabilités de tirer une bleue = 3/6.
Mais comment trouver le nombre total d'éventualités dans d'autres cas (jet de deux dés voir plus, pourcentages...). JIl me semble qu'il faut parfois multiplier d'autres fois additionner...
Merci.
Probabilités : trouver le nombre total d'éventualités
12 messages
- Page 1 sur 1
Désolé, je ne connais pas de méthode générale.
J'interviens juste pour le cas des tirages des boules.
Si on ne tire qu'une seule boule dans une urne contenant six boules, alors le nombre de cas est 6.
Mais si on en tire deux, alors il faut procéder à une multiplication, en faisant bien attention s'il y a ou non une remise dans l'urne de la première boule avant le tirage de la seconde.
Avec remise, le nombre de cas est 6 x 6.
Sans remise, le nombre de cas est 6 x 5.
Il ne faut pas hésiter à faire des petits dessins, des tableaux, imaginer des exemples sur la feuille de brouillon pour ne pas oublier de cas, ou pour ne pas en prendre trop.
J'interviens juste pour le cas des tirages des boules.
Si on ne tire qu'une seule boule dans une urne contenant six boules, alors le nombre de cas est 6.
Mais si on en tire deux, alors il faut procéder à une multiplication, en faisant bien attention s'il y a ou non une remise dans l'urne de la première boule avant le tirage de la seconde.
Avec remise, le nombre de cas est 6 x 6.
Sans remise, le nombre de cas est 6 x 5.
Il ne faut pas hésiter à faire des petits dessins, des tableaux, imaginer des exemples sur la feuille de brouillon pour ne pas oublier de cas, ou pour ne pas en prendre trop.
Pour les dés, le nombre de combinaisons possibles est de 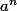 avec
avec  le nombre de faces des déset
le nombre de faces des déset  le nombre de dés lancés.
le nombre de dés lancés.
Mais les dés sont généralement à six faces donc le nombre de cas total est de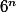
Remarque: lancés de
lancés de  dés équivaut à
dés équivaut à  lancés de
lancés de  dés.
dés.
Là tu confonds: soit A et B deux événements distincts,
Probabilité de A et de B:
Probabilité de A ou de B: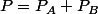
Exemple: Quelle est la probabilité de faire un 1, puis un 3 ou un 5 ?
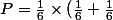=\frac {1}{18})
C'est ça que tu voulais savoir?
Mais les dés sont généralement à six faces donc le nombre de cas total est de
Remarque:
corder299 a écrit:Il me semble qu'il faut parfois multiplier d'autres fois additionner...
Là tu confonds: soit A et B deux événements distincts,
Probabilité de A et de B:
Probabilité de A ou de B:
Exemple: Quelle est la probabilité de faire un 1, puis un 3 ou un 5 ?
C'est ça que tu voulais savoir?
BancH, je ne comprends pas ton dernier message.
(EDIT: BancH a modifié son message par la suite)
corder299, la définition de "A et B sont indépendants" est : P(A et B) = P(A).P(B). En d'autres termes, par définition, A et B sont indépendants si P(A et B) = P(A).P(B).
Si A et B ne sont pas indépendants, alors il faut passer par les probabilités conditionnelles : P(A et B) = P(A sachant B).P(B)
Si A et B sont incompatibles (c'est-à-dire A inter B = ensemble vide), alors :
P(A ou B) = P(A) + P(B)
Si A et B ne sont pas incompatibles, alors on a la formule générale :
P(A ou B) = P(A) + P(B) - P(A et B).
(EDIT: BancH a modifié son message par la suite)
corder299, la définition de "A et B sont indépendants" est : P(A et B) = P(A).P(B). En d'autres termes, par définition, A et B sont indépendants si P(A et B) = P(A).P(B).
Si A et B ne sont pas indépendants, alors il faut passer par les probabilités conditionnelles : P(A et B) = P(A sachant B).P(B)
Si A et B sont incompatibles (c'est-à-dire A inter B = ensemble vide), alors :
P(A ou B) = P(A) + P(B)
Si A et B ne sont pas incompatibles, alors on a la formule générale :
P(A ou B) = P(A) + P(B) - P(A et B).
BancH, je me rends compte que tu as édité ton dernier message.
Tu as tout à fait le droit de penser ce que tu veux.
Néanmoins, j'ai aussi le droit de ne pas être d'accord avec toi.
1. Je ne pense pas que les notions d'indépendance et d'incompatibilité "coulent de source".
2. Je pense qu'il est impératif d'accompagner les formules du contexte/des hypothèses dans lesquels elles sont valides.
Cordialement,
Nicolas
Tu as tout à fait le droit de penser ce que tu veux.
Néanmoins, j'ai aussi le droit de ne pas être d'accord avec toi.
1. Je ne pense pas que les notions d'indépendance et d'incompatibilité "coulent de source".
2. Je pense qu'il est impératif d'accompagner les formules du contexte/des hypothèses dans lesquels elles sont valides.
Cordialement,
Nicolas
SpEED a écrit:En proba il n'existe pas vraiment de règles pour déterminer de genre de question.
Je suis bien d'accord.
SpEED a écrit: Si tu as bien compris le principe des arbres tu t'en sortiras toujours.
En effet, les multiplication par branches "sautent aux yeux" et tu détermines facilement ton nombre d'éventualités... :we:
Bonne chance pour la suite :id:
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
