Probabilités

par **hasnaefachtab** » 08 Juil 2006, 20:51

bonsoir

Cinq personnes ont le choix de cinq restaurants pour diner , elles choisissent au hadard.Quel est le nombr ede situations ou trois personnes se renconctrent et les autres ne se rencontrent pas??

oui j'ai deja posté mais je ne me rapelle plus ou je l'ai egaré.

en recalculant j'ai trouver 5 factorielle car on peut avoir
ABC D E
EDA B C
DEB C A
TEL ABCDE des personnes.

ai je juste cette fois? :mur:
merci

par **Sdec25** » 08 Juil 2006, 21:08

3 personnes sont dans le même resto et les 2 autres sont chacune dans un resto différent ?
Si on ne tient pas compte de l'ordre je dirais 3 possibilités.
exemple : les 3 premiers vont dans le resto 1, les 2 autres vont dans le resto 2 et 3
edit : j'ai mal lu ya pas que 3 restos

par **hasnaefachtab** » 08 Juil 2006, 21:13

ou bien le contraire 2 et 3 vont au restaurant 1 et 2

par **aviateurpilot** » 08 Juil 2006, 22:16

pour choisir les 3 restau

pour choisir les 3 presonnes qui se rencontrent

ces 3 personnes choisissent un des 3 restau est les deux autre chaque un va coisir un resau ou li y a

cas

donc :

par **BancH** » 09 Juil 2006, 00:08

Le groupe de trois personnes a le choix entre 5 restaurants, la quatrième personne a ensuite le choix entre 4 restaurants et la dernière a le choix entre 3 restaurants

Les cinq personnes peuvent interchanger leur place, tu multiplies alors par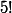

.

Mais lorsque les trois personnes du groupe de trois changent de place entre eux, il ne faut compter qu'une seule situation, il faut donc diviser le tout par

.

Il y a donc

situations possibles.

par **aviateurpilot** » 09 Juil 2006, 00:42

Banch a écrit:Le groupe de trois personnes a le choix entre 5 restaurants, la quatrième personne a ensuite le choix entre 4 restaurants et la dernière a le choix entre 3 restaurants
=>

là c'est bien
mais pour

Banch a écrit:Les cinq personnes peuvent interchanger leur place

là c'est faux
car tu as fait l'ordre dans la premiere formule que tu as trouvé

donc on parle plus de l'ordre
on va seulent utiliser une combinaison

donc

on pour ma formule

par **BancH** » 09 Juil 2006, 01:20

Je ne vois pas où est mon erreur, peut-être faut-il que je divise par 3 à la place de 3! ?

par **BancH** » 09 Juil 2006, 06:54

Je ne comprends pas cette phrase :

aviateurpilot a écrit:ces 3 personnes choisissent un des 3 restau est les deux autre chaque un va coisir un resau ou li y a cas

par **aviateurpilot** » 09 Juil 2006, 10:20

on peut supposer Le groupe des trois personnes comme une seule personne
dans ce cas on a 3 personnes et 3 restau:

là j'ai fait l'ordre
car quand j'ai choisi les 3 personne je n'ai utilisé qu'une combinaison ou il n y pas l'ordre.

la difference entre ta methode et la mienne
exemple:
combien de nombre de 3 chiffres differents de E={1,2,3,...,9}
ma methode: on prend 3 element de E sans ordre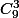

et apres on fait l'odre en mulipliant par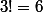

ta methode:

Banch a écrit:Le groupe de trois personnes a le choix entre 5 restaurants, la quatrième personne a ensuite le choix entre 4 restaurants et la dernière a le choix entre 3 restaurants

(là tu as fait l'ordre) pour le 1er chiffre : le choix entre 9 chiffre,pour le 2eme chiffres : le choix entre 8 chiffres,pour le 3eme chiffre : le choix entre 7 chiffre.
=>

est là c'est bien.
mais toi tu as refait l'ordre en multipliant par 5!/3!
dans ce exemple on muliplie par 3!
et tu trouve

ce qui est faux

par **BancH** » 09 Juil 2006, 11:35

D'après toi le calcul serait

?

par **aviateurpilot** » 09 Juil 2006, 12:12

donc

par **nox** » 10 Juil 2006, 15:39

aviateurpilot a écrit:on peut supposer Le groupe des trois personnes comme une seule personne
dans ce cas on a 3 personnes et 3 restau

pourquoi 3 restos?
5 restos!!

on choisit 3 personnes qui vont se retrouver parmi 5 ->

on choisit un resto parmi les 5 où le groupe de 3 va se retrouver -> 5 possibilités
Puis on place les 2 personnes restantes parmi les 4 restaurants -> 4*4

donc selon moi : 5*4*4*

PS : ou inversement on place les 2 personnes d'abord et le groupe de 3 ensuite ca donne le meme résultat

(5*4*3 + 5*4) *

par **Sdec25** » 10 Juil 2006, 16:09

Je comprends pas très bien pourquoi tu fais 4x4 nox.
Moi j'aurais dit :
3 personnes parmi 5 ->

1 resto pour les 3 ->

2 resto pour les 2 autres (sur 4) ->

Soit 300 possibilités.

par **nox** » 10 Juil 2006, 16:11

Sdec25 a écrit:2 resto pour les 2 autres (sur 4) ->

Non les 2 personnes qui restent peuvent tres bien se retrouver dans le même resto.

D'où mon 4*4...

800 possibilités au total

par **Sdec25** » 10 Juil 2006, 16:20

Ça fait 800 si les personnes peuvent se rencontrer, 300 sinon.
Mais c'est marqué que les autres ne se rencontrent pas.

par **aviateurpilot** » 10 Juil 2006, 16:55

Sdec25 a écrit:Je comprends pas très bien pourquoi tu fais 4x4 nox.
Moi j'aurais dit :
3 personnes parmi 5 ->
1 resto pour les 3 ->

là c'est bien
mais là:

2 resto pour les 2 autres (sur 4) ->

Soit 300 possibilités.

là c'est faux car tu dois encor multiplie par 2
car il y a 2 possiblité

dans

, et

dans

ou l'inverse
donc

et c'est le meme resultat que j'ai trouvé

nox a écrit:on choisit 3 personnes qui vont se retrouver parmi 5 ->

on choisit un resto parmi les 5 où le groupe de 3 va se retrouver -> 5 possibilités

là c'est bien
mais:

nox a écrit:Puis on place les 2 personnes restantes parmi les 4 restaurants -> 4*4

là c'est faux
1er personne a le choix entre 4 restau
2eme peronne a le choix entre 3 restau
donc c'est 4*3 pas 4*4

donc d'apres ta methode

et c'est le meme resultat que j'ai trouvé

par **Sdec25** » 10 Juil 2006, 17:30

Ah oui c'est parce qu'on tient compte de l'ordre.
Dans ce cas il faudrait plutôt faire

, comme tu viens de l'expliquer pour le

.
Même si on trouve le même résultat c'est mieux d'utiliser les A plutôt que les C (sauf pour choisir les 3 personnes).
On peut aussi faire

Et on trouve bien 600.

par **nox** » 10 Juil 2006, 17:54

ah oui exact je viens de voir que les autres ne se rencontrent pas ^^

Donc 600 en effet :)

par **aviateurpilot** » 10 Juil 2006, 21:42

donc mon premier resultat est vraie

par **Nicolas_75** » 15 Juil 2006, 04:09

Bonjour,

Je penche plutôt pour 1200.

Je copie/colle une réponse que j'ai donnée sur un autre forum.

L'énoncé me semble ambigu. Qu'est ce qu'une "situation" ?

Par exemple :
resto 1 = 3 personnes
resto 2 = 1 personne
resto 3 = 1 personne
est-elle la même situation que :
resto 1 = 3 personnes
resto 2 = 1 personne
resto 4 = 1 personne
Je suppose que non, et qu'il s'agit de situations différentes

De même :
resto 1 = A, B et C
resto 2 = D
resto 3 = E
est considérée comme une situation différente de :
resto 1 = A, D et C
resto 2 = B
resto 3 = E

J'appelle donc "situation" une correspondance entre les restaurants, chacun étant considéré comme discernable, et les personnes, chacune étant considérée comme discernable.

Dans ce cas, il faut d'abord répartir les 5 personnes en 3 groupes :
- groupe n°1 : 3 personnes,
- groupe n°2 : 1 personne,
- groupe n°3 : 1 personne
==>

possibilités

Ensuite, ces 3 groupes doivent être répartis dans les 5 restaurants :
==>

possibilités

Au total, je trouve donc :

possibilités.

Sauf erreur !

Nicolas

Probabilités

Probabilités

re

Qui est en ligne