Or il en a 20Mikou a écrit:c'est evidement pas 17^20 la solution ... si on prend un mec dans lascenceur il aura donc 1^20 = 1 facon de sortir, or il en a 17, parfois quand on en sait pas mieu vaut ne rien dire, merci.
Probabilités
57 messages
- Page 2 sur 3 - 1, 2, 3
mais l'on veut maintenant résoudre le problème si les personnes ne sont pas discernables.
=>soit
si les personnes ne sont pas discernables.
c comme si on cherche combien de facon peus t'on ecrire 17 sous forme de 20 nombres ou l'ordere de ces nombre est important
on suppose que
avec
on imagine qu'on a 17 boules rouge qui forme un petit segment [AB] et on veus mettre entre ces boules
à la fin on va trouver un nombre
=>donc le nombre de façon pour mettre les
c'est
et pour metter les 17-h "0" restant en multiplie par
donc le resultat final est :
aviateurpilot a écrit:on suppose queest le nombre des nombres different de 0
avec
h ne peut pas être égal à 1
il y aura au minimum 3 étages vides
et je ne suis pas convaincu par le raisonnement des boules...l'analogie ne me semble pas évidente...tu peux développer stp?
je suis d'accord avec les nombres...les h-1 boules noires représentent les signes + j'imagine...mais après je ne vois pas le lien...
Bonjour,
Si on considère que les personnes sont indiscernables...
Soit le nombre de personnes descendant à l'étage
le nombre de personnes descendant à l'étage  .
.
Ce problème revient à chercher le nombre (*) de 20-uplets différents) solutions de l'équation :
solutions de l'équation :

où les sont des entiers naturels
sont des entiers naturels
C'est un exercice classique. En considérant les ,
, 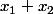 , ...,
, ...,  , cela revient également à :
, cela revient également à :
- dénombrer le nombre d'applications croissantes de |[1,19]| dans |[0,17]|
- dénombrer le nombre de 19-combinaisons avec répétition d'éléments de |[0,17]|
("19", puisque, de toute façon, le dernier est égal à 17)
est égal à 17)
Considérons les ,
, 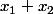 , ...,
, ...,  . Ils forment une 19-combinaison avec répétition d'éléments de |[0,17]|
. Ils forment une 19-combinaison avec répétition d'éléments de |[0,17]|
Considérons maintenant les ,
,  , ...,
, ...,  . Ils forment une 19-combinaison (classique) d'éléments de |[1,17+19]|
. Ils forment une 19-combinaison (classique) d'éléments de |[1,17+19]|
Il y en a donc :
Or il y en a autant que le nombre (*) cherché plus haut (bijection).
D'où le résultat :
Sauf erreur.
Nicolas
Si on considère que les personnes sont indiscernables...
Soit
Ce problème revient à chercher le nombre (*) de 20-uplets différents
où les
C'est un exercice classique. En considérant les
- dénombrer le nombre d'applications croissantes de |[1,19]| dans |[0,17]|
- dénombrer le nombre de 19-combinaisons avec répétition d'éléments de |[0,17]|
("19", puisque, de toute façon, le dernier
Considérons les
Considérons maintenant les
Il y en a donc :
Or il y en a autant que le nombre (*) cherché plus haut (bijection).
D'où le résultat :
Sauf erreur.
Nicolas
Nicolas_75 a écrit:C'est un exercice classique. En considérant les,
, ...,
, cela revient également à :
- dénombrer le nombre d'applications croissantes de |[1,19]| dans |[0,17]|
- dénombrer le nombre de 19-combinaisons avec répétition d'éléments de |[0,17]|
quand on parle de combinaisons avec répétition ca ne veut pas dire qu'on autorise la combinaison 17,17,17,17.....?
Nicolas_75 a écrit:C'est un exercice classique. En considérant les,
, ...,
, cela revient également à :
- dénombrer le nombre d'applications croissantes de |[1,19]| dans |[0,17]|
- dénombrer le nombre de 19-combinaisons avec répétition d'éléments de |[0,17]|
mais si j'ai bien compris (ce qui n'est pas certain ^^) tu dis que cela reviens à choisir 19 éléments parmi 17 avec répétition possible...
ces 19 éléments représentent les
EDIT : dsl d'avoir effacé le message nicolas_75 je voulais reformuler ca correctement
nox >> le nombre de séquences strictement ordonnées de  élements de
élements de  est justement égal à
est justement égal à 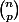

Pour plus de détails sur le nombre de solutions entières de telles équations, voir également :
http://maths-forum.com/showthread.php?t=4765&page=1&pp=10
Pour plus de détails sur le nombre de solutions entières de telles équations, voir également :
http://maths-forum.com/showthread.php?t=4765&page=1&pp=10
voila:
j'ai 17 boules rouges,quand on met les h-1 boules noir
c comme si je divise les boules par
et on trouve h nombre nombre
un nombre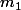 de boules rouge et une boule noir et un nombre
de boules rouge et une boule noir et un nombre  de boules rouge et une boule noir........et un nombre
de boules rouge et une boule noir........et un nombre  et une boules rouge noir et un nombre
et une boules rouge noir et un nombre  de boule rouge
de boule rouge
et on sais que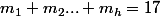
j'ai 17 boules rouges,quand on met les h-1 boules noir
c comme si je divise les boules par
et on trouve h nombre nombre
un nombre
et on sais que
nox a écrit:Bon de manière plus intuitive sans utiliser la loi multinômiale :
au premier étage on a soit 20, soit 19, soit......jusqu'à 0 personnes qui descendent. Appelons k1 le nombre de personnes descendues au premier étage. Au second, on a soit 20-k1, soit 20-k1-1, soit....jusqu'à 0 personnes qui descendent, et ainsi de suite.
Au final on trouve 7125 manières de répartir les gens :happy2:
mais j'avais inversé le nombre de personnes et le nombre d'étages...donc ensuite j'ai dit ca :
nox a écrit:apres correction je trouve 65536 (puissance de 2...ca me parait bizarre...mais bon...) en utilisant l'algorithme décrit un peu plus haut
edit : ca me parait faux...je suis en mode débug ^^
57 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 97 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
