Probabilités (BTS,lycée)

[BlackiStorm72]

Bonjour actuellement en BTS bioanalyse et contrôle, je bloque (et toute ma classe même le prof d'ailleurs ) sur cette exercice:

==> On considère un groupe de 3 étudiants. Quelle est la probabilité que l'un d'entre ait la même date d'anniversaire qu'un autre?

Notre professeur trouve 83% ce qui est impossible mais il n'en démord pas! A t-il raison car personne n'y croit cela voudrait dire qu'il y ait 83% de chances que j'ai la même date d'anniversaire que l'une des deux personnes assises à côté de moi en cours !

Aidez moi s'il vous plaît ( année avec 365 jours je précise ).
Merci

[Ericovitchi]

Bonjour, le plus simple est de calculer la probabilité qu'aucun d'entre eux n'ait la même date de naissance.
le premier a n'importe quelle date.
le second a 364/365 chances de ne pas avoir la même
le troisième a 363/365 chances de ne pas avoir la même que les deux autres.
la probabilité qu'ils aient 3 dates différentes est donc : (364/365)(363/365) ~ 0.99
la probabilité de l’événement contraire est donc 1-0.99 = 0.01

il n'y a donc que 1% de chance que l'un ait la même date de naissance qu'un des deux autres (et pas 83%)

[BlackiStorm72]

Bonjour, le plus simple est de calculer la probabilité qu'aucun d'entre eux n'ait la même date de naissance.
le premier a n'importe quelle date.
le second a 364/365 chances de ne pas avoir la même
le troisième a 363/365 chances de ne pas avoir la même que les deux autres.
la probabilité qu'ils aient 3 dates différentes est donc : (364/365)(363/365) ~ 0.99
la probabilité de l’événement contraire est donc 1-0.99 = 0.01

il n'y a donc que 1% de chance que l'un ait la même date de naissance qu'un des deux autres (et pas 83%)

Merci notre professeur avait fait ceci: ((3 parmi 365 )/ 365^3)=0,17, qu'avait-il calculé?
(nous on en avait déduit qu'il fallait faire 1-0,17 ensuite mais le résultat me paraissait impossible!

[Ericovitchi]

oui effectivement, il a dû essayer de faire le calcul en disant qu'il y a 365^3 triplet de dates possibles puis compter parmi ces dates le nombre de triplets qui ont 3 dates différentes. C'est le nombre de façons de choisir 3 objets distincts parmi 365 donc c'est

au total on a donc 8038030/365^3 = 16.53% (et il a pris le complément on se demande pourquoi ?)

mais ce calcul est trompeur car les événements ne sont pas disjoints. Voir http://fr.wikipedia.org/wiki/Paradoxe_des_anniversaires, c'est assez bien expliqué pourquoi.

C'est pour ça qu'il faut passer par l’événement contraire, on se trompe beaucoup moins.

[BlackiStorm72]

D'accord merci de ta réponse !
Bonne journée!

[zygomatique]

salut

ce n'est pas le problème d'être disjoints

on cherche un triplets d'entiers entre 1 et 365 (x, y, z) tel que x, y et z soient distincts !!!

il faut compter tous les triplets avec remise et compter ceux pour qui x , y et z sont distincts !!!

donc 365*364*363/(365*365*365) et on prend le complément à 1 ....


ce qui n'a rien à voir avec le nombre de parties d'un ensemble ....


ton prof de math est un bon à rien mauvais en tout ....

[BlackiStorm72]

salut

ce n'est pas le problème d'être disjoints

on cherche un triplets d'entiers entre 1 et 365 (x, y, z) tel que x, y et z soient distincts !!!

il faut compter tous les triplets avec remise et compter ceux pour qui x , y et z sont distincts !!!

donc 365*364*363/(365*365*365) et on prend le complément à 1 ....


ce qui n'a rien à voir avec le nombre de parties d'un ensemble ....


ton prof de math est un bon à rien mauvais en tout ....

Mdr merci par contre je comptais lui montrer le topic demain mais je crois qu'il va pas apprécier!

[Robic]

(Je réagissais au message d'Ericovitchi à 18h54, entre temps plusieurs messages sont apparus...)

et il a pris le complément on se demande pourquoi ?

Il croyait avoir calculé la probabilité que les trois dates soient différentes, or le but était de calculer la probabilité qu'au moins deux dates soient identiques. D'où le complémentaire.

Pour expliquer son erreur, je dirais que :
- Le calcul de "3 parmi 365" compte les sous-ensembles de trois dates. Ce ne sont pas des triplets ordonnés : dans un triplet ordonné, l'ordre importe ; pas dans un sous-ensemble. Exemple : {21, 35, 364} et {364, 21, 35}, c'est le même sous-ensemble, et le calcul de "3 parmi 365" compte ce sous-ensemble pour 1.
- Le calcul 365^3 compte, lui, des triplets ordonnés. Par exemple {21, 35, 364} est différent de {35, 364, 21}, qui comptent pour 2.

Si on veut faire un calcul correct, il ne faut pas tout mélanger. Par exemple calculons le rapport cas favorables / cas possibles avec des triplets ordonnés. Ici, il faut compter des triplets ordonnés de 3 dates distinctes, qui est un calcul non de combinaisons mais d'arrangements : il y en a 365x364x363. Autrefois on notait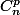 les combinaisons (p parmi n) et 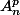les arrangements. Ton prof connaît peut-être cette notation, visiblement il a confondu les deux.

Ainsi, la probabilité d'avoir trois dates distinctes est = 0,9918. Le complémentaire (qui répond à la question) est donc 0,0082.

[BlackiStorm72]

(Je réagissais au message d'Ericovitchi à 18h54, entre temps plusieurs messages sont apparus...)


Il croyait avoir calculé la probabilité que les trois dates soient différentes, or le but était de calculer la probabilité qu'au moins deux dates soient identiques. D'où le complémentaire.

Pour expliquer son erreur, je dirais que :
- Le calcul de "3 parmi 365" compte les sous-ensembles de trois dates. Ce ne sont pas des triplets ordonnés : dans un triplet ordonné, l'ordre importe ; pas dans un sous-ensemble. Exemple : {21, 35, 364} et {364, 21, 35}, c'est le même sous-ensemble, et le calcul de "3 parmi 365" compte ce sous-ensemble pour 1.
- Le calcul 365^3 compte, lui, des triplets ordonnés. Par exemple {21, 35, 364} est différent de {35, 364, 21}, qui comptent pour 2.

Si on veut faire un calcul correct, il ne faut pas tout mélanger. Par exemple calculons le rapport cas favorables / cas possibles avec des triplets ordonnés. Ici, il faut compter des triplets ordonnés de 3 dates distinctes, qui est un calcul non de combinaisons mais d'arrangements : il y en a 365x364x363. Autrefois on notait les combinaisons (p parmi n) et les arrangements. Ton prof connaît peut-être cette notation, visiblement il a confondu les deux.

La probabilité d'avoir trois dates distinctes est donc = 0,9918.

D'accord! Merci

[paquito]

Il faut passer par l'événement contraire=on trouve don.C'est à partir de 30 étudiants,que l'on trouverait un résultat étonnant!