Probabilité

[beagle]

je laisse les autres répondre sur la formule, je la comprends, mais ne l'ayant jamais? apprise, ce n'est pas mon truc.

Juste dire qu'à ta question:
"Ce n'est pas ce que je veux dire, c'est par exemple, je lance 3 fois le dé, combien de chance j'aurai de faire un 1 ?"
Tout aussi important qu'une formule est de bien dire à quoi on répond.
Si tu veux un seul 1 sur les trois tirages, c'est la formule QS,
(entre parenthèse retrouvable à la main, c'est heureux)

Si tu fais trois tirages, trois lancers, et là tu te demandes ai-je augmenté ma proba d'avoir sorti le 1, alors la proba de sortie de 1 n'est pas la formule,
puisque la formule ne compte pas les doubles et les triples.Et le mieux est ce que je t'avais mis le 1-ça sort pas.

Voili voilou, une bonne question, bien précise, ou alors une réponse qui dit à quoi elle répond, plutot que des formules apprises par coeur et que l'on va essayer jusqu'à ce qu'une soit la bonne.
Si tu n'as pas encore appris cette formule, ton premier but est alors de comprendre ce qu'elle raconte,...

[Ericovitchi]

Il a raison, alors juste pour que tu comprennes la formule :
un évènement de probabilité p, il a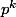 d'arriver k fois de suite
et qu'il n'arrive pas au cours de n-k coups restants c'est donc donc pour qu'un évènement arrive juste k fois au cours de n épreuve c'est mais si on dit ça on loupe quelque chose car on ne tient pas compte du fait que les événements qui marchent et ceux qui ne marchent pas peuvent arriver dans un ordre quelconque et donc il faut multiplier par le nombre de combinaisons c.a.d le nombre de façons que l'on a d'assembler k objets dans n objets et ce nombre c'est .

Donc une formule à vraiment savoir car elle est très utile :
Probabilité pour qu'un évènempent de probabilité p se produise exactement k fois au cours de n épreuves c'est :

[amix]

Vous pouvez faire un calcul, par exemple la probabilité a ce que 3 pommes tombent de l'arbre ? Je crois n'avoir pas compris

[beagle]

Vous pouvez faire un calcul, par exemple la probabilité a ce que 3 pommes tombent de l'arbre ? Je crois n'avoir pas compris

3 (k) pommes tombent de l'arbre sur les 5(n),
p=0,75 tombe, 1-p=tombe pas

si tu les numérotes, les ordonnes,
tu auras tombe 0,75
tombe pas 0,25
trois tombent sera toujours 0,75*075*0,75, donc 0,75 puissance k
et deux tombent pas sera toujours (1-0,75)*(1-0,75), donc puissance n-k
donc ce qui sera à multiplier pour la proba sera toujours ça.

mais maintenant il faut voir quelles pommes tombent ensemble.
si les trois premières
0,75*0,75*075*025*025
mais cela peut ètre la 1, la 4 et la 5
0,75*025*0,25*075*075
donc la proba 3 pommes tombe doit ètre additionné de tous les cas où cela tombe,
donc des combianaisons faisables de 3 dans 5,
le C(3,5), le C(k,n)

Au total tu dois multiplier le C(k,n) par la proba d'un seul évènement.

[amix]

3 (k) pommes tombent de l'arbre sur les 5(n),
p=0,75 tombe, 1-p=tombe pas

si tu les numérotes, les ordonnes,
tu auras tombe 0,75
tombe pas 0,25
trois tombent sera toujours 0,75*075*0,75, donc 0,75 puissance k
et deux tombent pas sera toujours (1-0,75)*(1-0,75), donc puissance n-k
donc ce qui sera à multiplier pour la proba sera toujours ça.

mais maintenant il faut voir quelles pommes tombent ensemble.
si les trois premières
0,75*0,75*075*025*025
mais cela peut ètre la 1, la 4 et la 5
0,75*025*0,25*075*075

Jusqu'a la je te suis, c'est après que je suis perdu, C (k,n) est égale a quoi ? Et la prop d'un seul évènement, c la proba que par exemple 3 pommes tombent ?

[beagle]

Jusqu'a la je te suis, c'est après que je suis perdu, C (k,n) est égale a quoi ? Et la prop d'un seul évènement, c la proba que par exemple 3 pommes tombent ?

Ericovitchi t'a mis la formule du C(k,n),
si tu maitrises peu ce truc, faut jouer avec sur des exemples et comme l'avait suggéré Gigamesh en faisant des dessins avec des arbres, des embranchements.

On va appeler T quand cela tombe, et A si la pomme reste accrochée à l'arbre,
les C(3,5)
sont les différentes associations de pommes qui tombent:
AATTT
ATATT
ATTAT
ATTTA
TAATT
TATAT
TATTA
TTAAT
TTATA
TTTAA

tu vois bien aussi que l'ordre de la multiplication de trois fois 0,75 et deux fois 0,25 importe peu, c'est cela la proba de base d'un des évènements.

[amix]

Hmm, je suis encore plus perdu, c (3,5) est égale a quoi enfaite ? Enfin pour le mutiplier par 0,75*025*0,25*075*075

[beagle]

http://fr.wikipedia.org/wiki/Coefficient_binomial

pour le C(3,5) fait le calcul:(1*2*3*4*5)/[(1*2*3)*(1*2)]
fait 10, les 10 combinaisons: AATTT, ATATT,...

0,75*025*0,25*075*075 est la combi:TAATT
cela représente un seul cas, et il y en a 10 à prendre en compte, d'où la multiplication par C(k,n), ici C(3,5)

[amix]

Ok merci je comprends

[amix]

Encore une question, après un calcule, la probabilité que 4 pommes tombent est d'environ 3% :

(5!/4!(5-4)!) * 0.75^4 * (1-0.75)^(5-4)
(120/256) * (81/256) * (1/4) = 9720/262144

9720/262144 est environ egale a 0.03

Cependant, si on calcule la probabilité a ce que sur les 5 pommes, 5 pommes tombent, ca serait p^5, 0.75^5 soit 243/1024, ou bien environ 0.23

Logiquement, il devrait y avoir plus de chances a ce qu'il est 4 pommes qui tombent, au lieu de 5 ? (je pense que c'est pas le bon calcul a faire pour calculer la probabilité a ce que toute les pommes tombent)

Une autre question, est ce que la somme des probabilité de l'ensemble d'évènements (1,2,3,4,5 pommes qui tombent) sont égale a 1 ?

[beagle]

Pour 4,
le C(4,5) donne 5,
donc on a:
p=5*0,75*0,75*0,75*0,75*0,25

et pour 5:
0,75 puissance 5

comme 5*0,25 est sup à 0,75,
avec 4 la proba est sup à 5

mais la logique du nombre de pommes qui tombe, j'ai pas réfléchi, mais attention, tu as pris une proba élevée de chute, 0,75


Pour l'ensemble de 1, 2,3,4,5 pommes tombent,
cela ne réalise que l'ensemble des pommes qui tombent,
donc il manque les 5 pommes ne tombent pas:
donc c'est 1-0,25 puissance 5

[amix]

Oui en effet, j'ai oublié la probabilité qu'aucune pommes ne tombent

Et pour l'autre calcule, ou j'ai fait une erreur, autant pour moi.

Merci a tous pour vos réponses

[Eleve222]

Bonjour
il faut préciser: avoir exactement 1 fois la face n°1 ou au moins une fois la face n°1
pour le premier cas: si on lance n dés, la probabilité d'avoir exactement une fois la face1 est égale à: (combinaison de 1 parmi n )*(1/6)*(5/6)^(n-1).
pour le deuxième cas : 1-(5/6)^n
bonne chance
vous pouvez visiter ce site http://www.sigmaths.co.cc et plus précisément la page suivante http://www.sigmaths.co.cc/series/proba/proba0.php, il y a une mine d'exercice corrigés de probabilité

[flou555]

bonjour,

je me suis inscrit sur ce forum à la suite d'un pari, j'ai besoin d'aide.
la question est simple :
dans le cadre d'une succession de lancés d'un dé non pipé à 6 faces, puis-je affirmer que, si je n'ai pas obtenu de 6 avant le sixième lancé :
"la probabilité d'obtenir un 6 au sixième lancé est de [1-(5/6)^6]" ?

merci d'avance !