[Math] Probabilité Problème.

[Suieton]

Bonjour , quelqu'un pourrait me dire comment résoudre ce problème svp ?

----> Une agence fabrique une arme qui a une probabilité de 0,7 d'atteindre sa cible.
Combien faut-il de tir pour que la cible soit détruite avec une probabilité de 0,99 ?

Merci d'avance

[L.A.]

Bonjour,

Quelle est la probabilité que la cible ne soit pas détruite en 1 essai ? 2 essais ? 5 essais ? etc...

A partir de quel nombre d'essais cette probabilité est elle inférieure à 0,01 ?

[Al-Kashi]

Bonsoir,
Soit le nombre de balles ayant atteints la cible à l'issue de tirs.
Si les tirs sont identiques et indépendants, alors suit une loi binomiale de paramètres et .
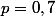
La cible est détruite si elle est touchée au moins une fois, c'est donc l'événement .

D'autre part,

Ainsi, il faut au moins tirs ....
NB: si tu ne connais pas la fonction ln, un tableau de valeurs suffira

Remarque: Il aurait été préférable que l'énoncé demande que la probabilité soit au moins égale à .