Bonjour,
Une petite difficulté à résoudre ce problème.
Une machine à café débite en moyenne 55 ml. Sur celle ci il est marqué qu'elle délivre 50ml.
10% des tasses ont moins de 50ml. Le débit suit une loi normale.
comment déterminer l'écart type sigma ?
Mon raisonnement est le suivant :
p(débit<50ml)=0,1 et moyenne = 55.
Je parviens à trouver par tâtonnement sigma = 4 avec ma calculatrice.
Peut on déterminer sigma littéralement ?
Merci par avance
Probabilité loi normale
3 messages
- Page 1 sur 1
Bonjour ! Si j'ai bien compris, on a une loi normale de moyenne 55 ml et on ignore l'écart-type. Mais on sait que 10 % des tasses font moins de 50 ml. Du coup 10 % des tasses font plus de 60 ml je suppose.
J'ai appris les stats à une époque où on utilisait encore des tables (mais je sais qu'on en utilise encore en fac de médecine et dans certains BTS), donc la méthode qui suit s'en inspire, mais les calculatrices modernes permettent probablement de faire le calcul en appuyant sur la bonne touche.
Je note F la fonction de répartition de la loi normal centrée réduite, c'est-à-dire F(t) = P(Z <= t) où Z suit la loi normale centrée réduite.
Par exemple :
F(0) = 0,5 ;
F(1,96) = 0,975 (car entre -1,96 et 1,96 on a 95 %, et 2,5 % de part et d'autre) ;
F(2,58) = 0,995 (car entre -2,58 et 2,58 on a 99 %, et 0,5 % de part et d'autre).
Notons X la variable aléatoire correspondant à la quantité de café. Elle suit la loi normale de moyenne 55 ml et d'écart-type inconnu, et on sait qu'il y a 10 % des tasses qui ont moins de 50 ml donc, par symétrie, 10 % des tasses ont plus de 60 ml.
Autrement dit : = 0,9)
On fait un centrage-réduction :
 = P(\frac{X - 55}{\sigma} \leq \frac{60-55}{\sigma}) = 0,9)
c'est-à-dire :
 = 0,9)
 = 0,9)
On lit alors dans la table le nombre t qui correspond à F(t) = 0,9 (ou bien on utilise la calculatrice) et on en déduit que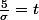 d'où la valeur de
d'où la valeur de  .
.
J'ai appris les stats à une époque où on utilisait encore des tables (mais je sais qu'on en utilise encore en fac de médecine et dans certains BTS), donc la méthode qui suit s'en inspire, mais les calculatrices modernes permettent probablement de faire le calcul en appuyant sur la bonne touche.
Je note F la fonction de répartition de la loi normal centrée réduite, c'est-à-dire F(t) = P(Z <= t) où Z suit la loi normale centrée réduite.
Par exemple :
F(0) = 0,5 ;
F(1,96) = 0,975 (car entre -1,96 et 1,96 on a 95 %, et 2,5 % de part et d'autre) ;
F(2,58) = 0,995 (car entre -2,58 et 2,58 on a 99 %, et 0,5 % de part et d'autre).
Notons X la variable aléatoire correspondant à la quantité de café. Elle suit la loi normale de moyenne 55 ml et d'écart-type inconnu, et on sait qu'il y a 10 % des tasses qui ont moins de 50 ml donc, par symétrie, 10 % des tasses ont plus de 60 ml.
Autrement dit :
On fait un centrage-réduction :
c'est-à-dire :
On lit alors dans la table le nombre t qui correspond à F(t) = 0,9 (ou bien on utilise la calculatrice) et on en déduit que
Résolution
Merci,
J ai progressé de mn côté.
Votre solution est la bonne.
Dans le raisonnement,
V=volume de café
v=(V-55)/sigma. Je fais un chgt de variable
Je cherche ds le tableau 0.9 ( pas 0,1 qui n'existe pas forcément - on prd le complémentaire)
La valeur trouvée ds le tableau ( multipliée par moins 1- à cause de la recherche complémentaire) correspond effectivement à (50-55)/sigma.
Il reste à résoudre et c'est ok
Merci beaucoup
J ai progressé de mn côté.
Votre solution est la bonne.
Dans le raisonnement,
V=volume de café
v=(V-55)/sigma. Je fais un chgt de variable
Je cherche ds le tableau 0.9 ( pas 0,1 qui n'existe pas forcément - on prd le complémentaire)
La valeur trouvée ds le tableau ( multipliée par moins 1- à cause de la recherche complémentaire) correspond effectivement à (50-55)/sigma.
Il reste à résoudre et c'est ok
Merci beaucoup
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
